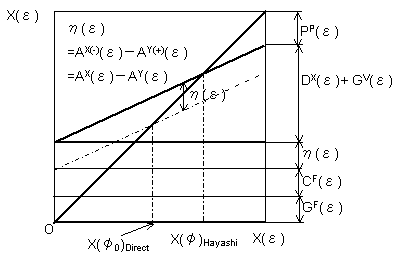
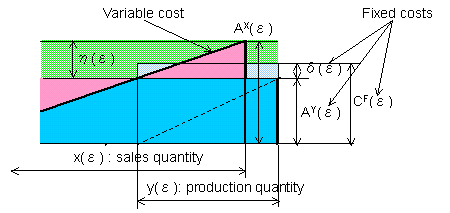
Fig.2-5 in §2 Hayashi's break-even chart under absorption costing
PP (ε) = QM (ε) + AX (ε) – η (ε) – CF (ε) – G (ε)
PP (ε) = X (ε) – DX (ε) – AX (ε) – δ (ε) – GF(ε) – GV (ε)
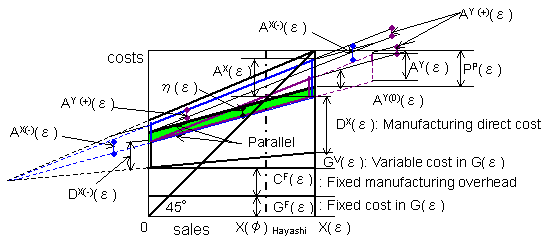
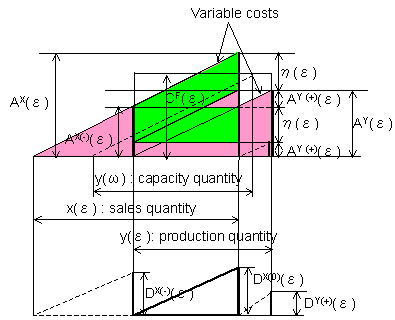
Fig. 5-2 Grounds for deriving Fig.5-1
X (φ) / X (ε)
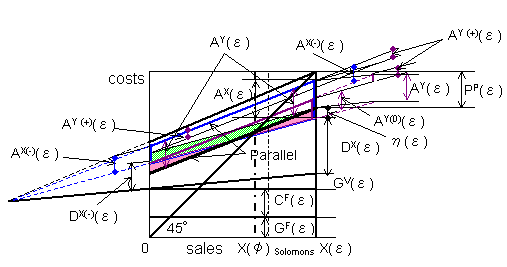
| §6 The cause of Solomons's error in his break-even chart for absorption costing | |
| The author's break-even chart shown in Fig.5 in §2 under absorption costing is very simple but its derivation is very difficult. Solomos's paper was presented in 1968. Since then his theory was adopted in many accounting textbooks. Many academic experts in accounting must have checked his derivation of the formula. However, nobody could find the error in his formula. The author's paper was also rejected by a Japanese accounting academy and he lost his opportunity to make his theory public. | |
|
|
|
|
Fig.2-5 in §2 Hayashi's break-even chart under absorption costing |
|
| However, if it remains in textbooks, Solomos's theory could be considered harmless, even if it is wrong, because his chart is expressed with goods quantities on the horizontal axis and monetary costs on the vertical axis, and therefore can't be utilized in real business situations. After the application of this specification in §2, the author (Hayashi) began to study economics and found an error in the investment multiplier effect formula by J.M.Keynes. | |
| The author (Hayashi) has noticed that the public imagines that the inventories (monetary unit ) line of manufacturing goods crosses with the 45° line( goods supply line ) with a slope, and the difference between both lines is explained as excess supply i.e. an increase of goods inventories. This is wrong. The author considers its cause as follows. Although during Keynes's era the shape of the demand line, which included inventories, could not be imagined graphically, the following graphical expression by Solomos was such that manufacturing overhead was not constant with respect to goods sales (this is incorrect). In addition, Solomons's theory was very difficult to understand and was not expressed with monetary units. Hence, it is important to show Solomos's error graphically with monetary units in economics. | |
| The notations used in §2 are presented in the following: | |
| X(ε) : Sales at the end of an accounting period | |
| AX (ε) = AX(–)(ε) + AX(0)(ε) : Manufacturing-overhead-applied | |
| = AX(–)(ε) + AY (ε) – AY(+) (ε) | (2-1) |
| Superscript X : Expressing manufacturing cost of goods sold | |
| Superscript Y : Expressing manufacturing cost of goods produced | |
| Superscripts – , 0, + : Refer to Fig.1 in §1. | |
|
η
(ε)
=
AX(–)(ε)
–
AY(+)
(ε) |
|
| = AX (ε) – AY (ε) | (2-2) |
| DX (ε) : Actual manufacturing direct cost | |
| EX (ε) = DX (ε) + AX (ε) : Manufacturing full cost | (2-3) |
| QM (ε) = X (ε) – EX (ε) : Managed gross profit | (2-4) |
| δ (ε) = CF (ε) – AY (ε) : Cost variance | (2-5) |
| Q (ε) = QM (ε) – δ (ε) : Sales gross profit | (2-6) |
| (2-7) | |
|
PP (ε) = QM (ε) + AX (ε) – η (ε) – CF (ε) – G (ε) |
|
| = X (ε) – DX (ε) – η (ε) – CF (ε) – G (ε) | (2-8) |
| We divide G (ε) as follows: | |
| G(ε) = GF (ε) + GV (ε) | (5-1) |
| where GF (ε) = fixed cost in G (ε) and GV (ε) = variable cost in G (ε). Thus we have | |
| PP (ε) = X (ε) – DX (ε) – η (ε) – CF (ε) – GF (ε) – GV (ε) | (5-2) |
| or | |
| PP (ε) = X (ε) – DX (ε) – AX (ε) + AY(ε) – CF (ε) – GF(ε) – GV (ε) | (5-3) |
| Substituting Eq.(2-5) into (5-3) gives: | |
|
PP (ε) = X (ε) – DX (ε) – AX (ε) – δ (ε) – GF(ε) – GV (ε) |
(5-4) |
| Both Eq.(5-2) and Eq.(5-3) are the same. | |
| The author( Hayashi) regarded [ η (ε) + CF (ε) + GF (ε) ] in Eq.(5-2) as the fixed cost terms, and made a break-even sales formula using the following relationship: | |
| X (φ) = fixed costs / ( X (ε) – variable costs) | (5-5) |
| where X (φ) = beak-even sales. Therefore, the author obtains the following break-even sales formula : | |
| X (φ) / X (ε) = ( η (ε) + CF (ε) + GF (ε)) / (X (ε) – DX (ε) – GV (ε)) | (2-19) |
| If η (ε)=0, we obtain the conventional break-even formula where the manufacturing-overheads-applied don't change the position of the break-even point. | |
| The chart for Eq(2.19)is shown in Fig.5-1 and the grounds for the chart is presented in Fig.5-2. | |
|
|
|
| Fig. 5-1 Break-even sales by the author( Hayashi) | |
|
|
|
|
Fig. 5-2 Grounds for deriving Fig.5-1 |
|
| On the other hand, Solomons regarded [ δ (ε) +GF(ε) ] as the fixed cost term, and so he obtained: | |
| X (φ) / X (ε) = ( δ (ε) +GF(ε) ) / (X (ε)– DX (ε) – GV (ε) – AX (ε) ) | (5-6) |
| After this operation, he substituted Eq.(2-5) into Eq.(5-6) , and he obtained: | |
|
X (φ) / X (ε) |
|
| = ( – AY(ε)+ CF(ε) + GF(ε) ) / (X(ε) – DX(ε) – GV(ε) – AX(ε) ) | (2-23) |
| What is the difference between the author's chart and Solomons's one for the break-even sales under absorption costing? In Eq.(2-19), η (ε) is a fixed cost as the difference between the two variable costs AX(ε) and AY(ε). On the other hand, in Eq.(2-23), AY(ε) in η (ε) is a fixed cost (minus value) and AX(ε) in η (ε) is a variable cost. The treatment of AY(ε) as a fixed cost resulted from the fact that δ (ε) was regarded as a fixed cost by Solomons. Thus, we have the following graphs with overdrawing for Solomons's break-even chart under absorption costing. | |
 |
|
| Fig. 5-3 Solomons's break-even sales | |

|
|
| Fig. 5-4 Grounds for deriving Fig.5-3 | |
| If η (ε)=0 in Eq.(2-23), the remaining manufacturing-overhead-applied terms change the position of the break-even point. This contradicts the knowledge in direct costing. That is to say, when η (ε) = AX (ε) – AY (ε) =0, we have the same expression X (ε) = PP (ε) + DX (ε) + CF (ε) + GF (ε) + GV (ε) at the point X =X(ε) in both cases of Solomons and the author. At the same time, we obtain PP (ε) = X (ε) – variable terms [DX (ε) + GV (ε)] ) – fixed terms [(CF (ε) + GF(ε)] from Eq.(5-2) in the author's case; on the other hand, in Solomons's case, we have PP (ε) = X (ε) – variable terms [(DX (ε) + AX(ε) ) + GV (ε)] – fixed terms [(CF (ε) –AY(ε) + GF(ε)]. In this case, the origin of DX (ε) and AX(ε) is the same. Consequently, if we draw the break-even charts of those two cases, the break-even sales points are different from each other. | |
| Both Fig.2-5 and Fig. 5-1 are the same. Fig.2-5 is very simple, but the ground covered is how difficult and complicated! | |
9/April/2007