η (ε) = AX(-) (ε) - AX(+)(ε)
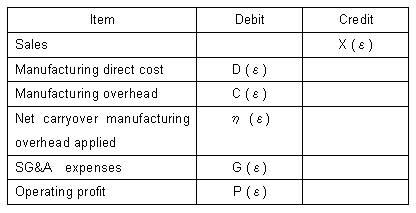

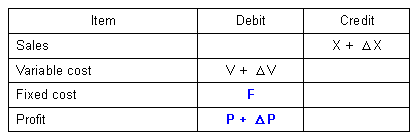
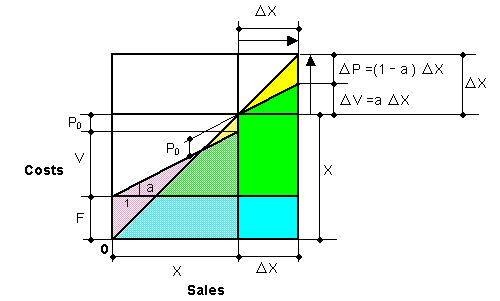

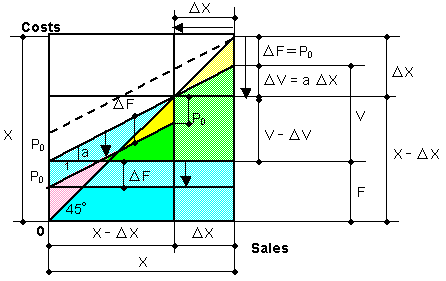

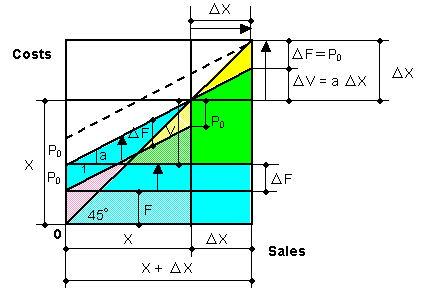

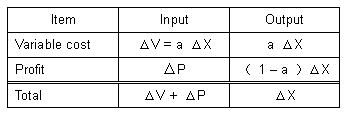
Table 7 Relationship between incremental inputs and output when Δ F = 0
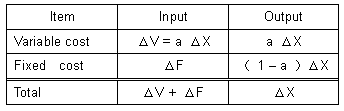
Table 8 Relationship between incremental inputs and output when Δ P = 0
§8 Preparation for economics November 2003 Yuichiro Hayashi
|
|
||
| Please refer to 'Outline of This Website'. The income statement Table 1 in the website, is changed to Table 1 below, where: | ||
|
η (ε) = AX(-) (ε) - AX(+)(ε) |
(1) | |
| Table 1 Income statement of a company | ||
|
|
||
| Table 1 is transformed to Table 2, where the notation (ε) has been omitted, and: | ||
| V( variable cost) = D ; which mainly consists of the amount paid to sub-constructors, variable labor costs, and material costs. | ||
| F = C + η +G ; Fixed cost. | ||
| Table 2 Income statement-2 | ||
|
|
||
| In the income statement-2 in Table 2, we will examine the break-even chart when sales X naturally increases or decreases to be X + Δ X, keeping F constant. The expected income statement is obtained as shown in Table 3. | ||
| Table 3 Income statement when F = constant | ||
|
|
||
| From Table 2 and Table 3 we have: | ||
| Δ X = Δ V + Δ P | (2) | |
| When we denote a = V / X ( Variable cost ratio), Eq. (2) is expressed as follows: | ||
| Δ X = a Δ X + Δ P | (3) | |
| Then we get: | ||
| Δ P = (1 - a ) Δ X | (4-1) | |
| Δ X = Δ P / (1 - a ) | (4-2) | |
| Table 3 is transformed into Fig. 1. In Fig. 1, Δ X takes any value, or we can give any value to Δ X. Ratio Δ P / Δ X = 1 - a . Eq. (2) holds whether Δ X moves in the plus or minus direction. Eq. (2) shows that the incremental sales consist of the incremental profit and the incremental variable cost. Eq. (4-2) indicates that Δ X can be expressed by using Δ P and ' a '. This equation does not mean that Δ P is naturally multiplied by 1 / (1 - a ) to be Δ P / (1 - a ). Both Δ P and Δ V are variable energy inputs as explained later. The expression Δ P / (1 - a ) is another expression of Δ X, in the same meaning, the expression Δ V / a =Δ X is. | ||
|
|
||
| Fig. 1. Break-even chart when X → X + Δ X and F = constant | ||
| There is another case that the current, fixed cost F needs to decrease in such a manner that the current profit P is kept constant when the next year's sales are expected to decrease as much as Δ X because of recession. In this case, profit P is set to be constant, that is P = P0, in Table 2. The next year's intended income statement is shown in Table 4. | ||
| Table 4 Next year's intended income statement | ||
|
|
||
| From Table 2 and Table 4 we have: | ||
| Δ X = Δ V + Δ F | (5) | |
| Δ X = Δ F / (1 - a ) | (6) | |
| This case is shown in Fig. 2. In this case, the decrement Δ X consists of a proportional part of Δ X and an independent part of Δ X. The former is Δ V = a Δ X , and the latter is Δ F = P0. The figure shows that the total costs decrease as much as Δ F + Δ V, and the sales decrease as much as, Δ X keeping P constant. | ||
|
|
||
| Fig. 2 Break-even chart when X → X - Δ X , keeping P constant | ||
| Consider the case where Δ F is a given amount in F → F + Δ F keeping P( = P0) constant, that is Δ P = 0. In a similar manner as the previous case, we have Table 5 and a break-even chart Fig. 3 for Table 5. In this case, Δ F = P0 holds. | ||
| Table 5 Income statement when F → F + Δ F, keeping P constant | ||
|
|
||
|
|
||
| Fig. 3 Break-even chart when X → X + Δ X, keeping P constant | ||
| In Fig. 3, we should not interpret as if F → F + Δ F( = P0 ) and that Δ X, therefore, naturally approaches P0 / (1 - a ). Fig.3 should be interpreted as if F → F + Δ F( = P0 ). The next year's sales X need to increase to be X + P 0 / (1 - a ) in order to keep P constant . This result will not be necessarily assured because there is no relationship between incremental fixed costs and incremental sales in the firms, when P cannot be kept constant. | ||
| The relationship between Δ X (sales= goods sold, output), Δ N (inventory, goods not sold, output ), Δ P (profit, input), Δ V'( injected variable costs, input), and Δ F'( injected fixed costs, input) will be studied a little more deeply. By the principle of conservation of energy, that is, Input energy ( Injected energy into goods ) = Output (produced goods with the energy ), we have: | ||
| Δ X + Δ N = Δ P + Δ V' + Δ F' | (7) | |
| where the left side shows output and the right side, input energy. | ||
| If we define: | ||
| Δ N = Δ V' + Δ F' - (Δ V + Δ F ) | (8) | |
| we obtain : | ||
| Δ X = Δ P + Δ V + Δ F | (9) | |
| where | ||
| Δ V = a Δ X | (10) | |
| a = V / X | (11) | |
| In firms' income statements, Δ N is capitalized to be assets. Δ X is sales. The injected energy Δ P means that Δ P is incremental energy evaluated or evaluated value by buyers. Δ V is a variable cost including labor costs, amount paid to sub-contractors and the other variable costs. The term 'fixed' in 'fixed cost' means that the cost does not relate to the increase and decrease of sales Δ X. Therefore, the fixed cost can vary independently of sales or unaffectedly by sales fluctuation. | ||
| The relationship between the terms in Eq.(9) is obtained by Table 6. | ||
|
|
||
| Table 6 Relationship between incremental inputs and output in firms | ||
| Table 6 shows firstly that Δ X( output) is determined by demand after negotiations with buyers. Secondly, variable input energy Δ V =a Δ X is automatically needed to produce Δ X. Thus, Δ P and Δ F have a competing relationship for sharing Δ X - Δ V. Thirdly, entrepreneurs determine the amount of Δ F not affected by the amount of Δ X, by the definition of the fixed cost. The residual value( evaluated cost by the buyers) is Δ P. | ||
| Through these tables, we have the following: | ||
| Case-1 When F is constant, that is to say Δ F = 0, we have Table 7. | ||
|
|
||
|
Table 7 Relationship between incremental inputs and output when Δ F = 0 |
||
| In Table 7 the following holds: | ||
| Δ P = (1 - a ) Δ X | (12-1) | |
| Δ X = Δ P / (1 - a ) | (12-2) | |
| The expression Δ P / (1 - a ) is another expression of Δ X. This shows that Δ P (input) is directly proportional to Δ X (output). These relations are expressed in Fig. 1. | ||
| Case-2 When P is constant, that is to say Δ P = 0, we have Table 8. | ||
|
|
||
|
Table 8 Relationship between incremental inputs and output when Δ P = 0 |
||
| In table 8 the following holds: | ||
| Δ F = (1 - a ) Δ X | (13-1) | |
| Δ X = Δ F / (1 - a ) | (13-2) | |
| Eq. (13-1) shows that if Δ X (output) is given as a determined amount, Δ F( input energy) will be determined according to Δ X. So, Δ F is not independent of the amount of Δ X under the condition of keeping P constant. If F varies a little from Eq. (13-1), Δ P will inevitably be generated a little. Therefore, the condition of both Eq. (13-1) and Δ P = 0 is one pair in Table 8. | ||
| Case-3 In the case of Table 6 , we have: | ||
| Δ P = (1 - a ) Δ X - Δ F | (14) | |
| When Δ X (output) is a given amount. Δ P and Δ F make a linear relation which will be explained later. | ||
| There is another case where the ratio a (= V / X) itself varies. However, we will not pursue this further. Through the cases, we know that the income statement expresses the relationship between input energy ( costs and profit) and output (sales). | ||
| In conclusion, cost-volume-profit analysis under standard costing (absorption costing or full costing) is possible. | |||