![]()
音楽室(予備知識編)
![]()
[ 予備知識編/音程 ・音列構造の理解の一助として ]
この”音楽室”なる項目において私が取り上げようとしているのは、いわゆる現代音楽系の作曲に関するものであり、とりわけそれは12音音楽の成立以降、それを作曲技法の面からいえば12音技法、音列技法などと呼ばれる作曲法から出発する事になろう。
ヨーロッパ伝統の和声法が崩壊してより散逸したままであった平均率半音階の12の音は、その後程なくしてスクリャービンやロスラヴェッツ、ゴリシェフ等によって作曲の上で扱われている。しかしながら、12の半音による作曲法において、より普遍的、有効な方法として音楽史上に効力を発揮するのはさらに時間が必要であった。それを具体的にいえば12音音列の現われるのを待たねばならなかったという事である。
この音列というものは単に音そのものを並べて順列化したものというより、本質的にはその音の順列によって生ずる音程関係の順列という事が出来よう。よって、この音列というものについて思索の対象とする場合、必然的に音程に関してのそれなりの理解(特に読み取る力量)をある程度は身に付けていることが望ましい。したがって、12音技法を取り上げるに先立って、ここに理解のための予備知識として音程(少なくとも音列構造を理解するに足る程度のレベルとして)に関しての記事を記す事とした次第である。
このページはそのような意義を持つ性格上、もしあなたが音程に関して一定の理解を持たれている場合は、読み飛ばしていただいても一向に差し支えないのである。
まずはじめに、12音技法における記譜について若干ふれておかねばならないであろう。
この技法においては従来のヨーロッパ伝統音楽の5線記譜法を援用するのが一般的である。もとよりこの記譜法は、本質的にいって12音音楽にはそぐわないものではあるが、我々はこの記譜法にあまりにも慣れてしまっている。したがって、いまだかつて12音技法のための何らかの記譜法が一般化した事例は見当たらない(実際にあったとしてもそれは作曲家個人のものに限られる)。それはたとえ12音技法にはそぐわないといえども、多少の不便はあるにせよどちらも同じく12の半音を扱うのであり、その共通項において援用し得るものであって、全く新しい12音のための統一的記譜法の確定と、その普及・標準化の困難さを思い合わせた場合、その意味で妥協しつつ、今日に至るまで12半音階を扱う場合、ほとんどの場面で従来どおりの5線記譜法が用いられてきた。よってこの項目においてもそのような一般性を重視して、便宜の上から音程や音列の譜例等においては伝統的な5線記譜法にしたがう事にする。
・音程の度数
音程とはある一組の音の高さのへだたりを表現するための尺度であり、それは”度数”、そしてそれに付記される”完全”、”長”、”短”、等のことばによって表される。
例えば、EとAとの2つの音がある場合、この音程を”4度”であるという。なぜならば、この2音は4つの幹音(#やbの付かない音。ピアノの白鍵にあたる音)にわたっているからである。
![]()
CとHとの音程を”7度”という。この場合7つの幹音にわたっているからである。また、同じ幹音どうしの2音の場合は”1度”と数える。

度数そのものの数え方は、それらの音に#やbなどの変化記号が付いていても変わらない。
・単音程と復音程
完全8度(オクターブ)の範囲までの音程を”単音程”という。これは全ての音程の基礎となるものである。また、完全8度をこえる音程を”復音程”という。このような音程は、つまり”オクターブ+単音程”という状態のものである。
例えば9度音程は、1オクターブ(完全8度)+2度であり、10度音程は、1オクターブ(完全8度)+3度、12度音程は、1オクターブ(完全8度)+5度である、等々。しかし12音技法の場合、このような復音程という尺度を持ち込むのはあまり意味がない。音列の構成音はその性格上、いかなるオクターブの位置をも取り得る。例えば9度の場合は単に2度音程をなす音がオクターブ上に移高された同一のものと解釈される。12音技法に関わるのはもっぱら単音程の方である。
・音程における完全・長・短等の種類について
音程の度数が同じでも、その一組の音に#やbなどの変化記号が付く場合があり、それは幹音のみによる音程とは性格が異なる。そのような事から、それぞれの性質と区別のために以下のことばを音程の度数と併用して用いるのである。
”完全”・”長”・”短”・”増”・”減”・”重増”・”重減”
しかしこれらの語はいかなる音程に対してでも同じように用いられるものではなく、”完全系の度数”と”長短系の度数”との2つの系列において異なるのである。
・完全系音程における度数
完全系の度数は1度、4度、5度、8度であり、その完全音程をこれらの標準的な状態とし、その度数において音程が1半音分広い場合は”増”とし、逆に1半音分狭い場合は”減”とする。ただし、1度音程においては”減”の状態は生じない。1度とは全く同一の高さ(同度・ユニゾン)の音程であり、その状態を完全1度と定めているのであって、それよりも狭い音程(減1度等)は存在しない。
・長短系音程における度数
長短系の度数は2度、3度、6度、7度であり、”長”、もしくは”短”の状態を標準とし、”長”よりも音程が半音分広い場合は”増”であり、半音分狭い場合は”減”を用いる。
そして重要な事は、完全系の度数が”長”音程あるいは”短”音程になる事はなく、また長短系の度数が”完全”になることは有り得ないという事である。
・”完全系音程”、”長短系音程”の2つの音程系列の関係
以下の図1.は完全系、長短系の2つの系列がどのような関係となっているのかを簡単に示したものである。広い・狭いの単位は半音である。
図1.
| 広い> [ 完全系 ] >狭い | |||||
| 重増> | 増> | 完全 | >減 | >重減 | |
| 1・4・5・8度 | |||||
| : | |||||
| 長 | 短 | ||||
| 2・3・6・7度 | |||||
| 広い> [長短系 ] >狭い | |||||
この図式によればいずれの系列においても、半音1つ分広がれば図の左方向へ1段階移動し、半音1つ分狭まれば右方向へ1段階移動する。例えば完全5度が半音1つ分狭まれば”減5度”となり、短6度が半音1つ分広がった場合には”長6度”となる。
以下の譜例は完全系音程であり、aは完全5度である。その他の音程も5度系であるが完全5度とは異なる。図1.を参考にみてみよう。
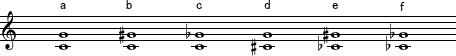
bはG音に#が付き、もとの音程よりも半音1つ分広くなったので”増5度”である。
cはG音にbが付き、もとの音程より半音1つ分狭くなったので”減5度”である。
dはC音に#が付き、もとの音程より半音1つ分狭くなったので”減5度”である。
eはG音に#、C音にbが付き、各々半音1つ分、全体で半音2つ分(1全音)広くなったので”重増5度”となる。
fはC音、G音ともにbが付き、もとの音程(a)と変わらない。したがって”完全5度”である。
このような関係は他の完全系音程である1度、4度、8度についても同様である。
以下の譜例は長短系音程であり、aは長3度である。その他の音程も3度系であるが長3度とは異なる。この場合図1.の長短系の図式に注目しなければならない。
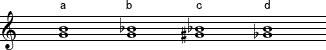
bはもとのH音にbが付き、半音1つ分狭くなっているので”短3度”である。
cはH音にb、G音に#が付き、各々半音づつ、全体で半音2つ分(1全音)狭くなっているので”減3度”である。
dはG音にbが付き、半音1つ分音程が広くなっている。したがって”増3度”である。
このような関係は他の長短系音程である2度、6度、7度についても同様である。
・2つの幹音によってできる音程
2つの幹音によってできる音程は、全ての音程の基礎となるものであり重要である。また、このタイプの音程は種類も限られているので、これを習得するのは比較的容易である。
以下の音程はいずれも完全1度である。

以下の音程は2度音程であるが、E-F, H-Cのみ短2度であり、他は全て長2度である。

以下の音程は3度音程であるが、C-E, F-A, G-Hのみ長3度であり、他は全て短3度である。

以下の音程は4度音程であるが、F-Hのみ増4度であり、他は全て完全4度である。

以下の音程は5度音程であるが、H-Fのみ減5度であり、他は全て完全5度である。

以下の音程は6度音程であるが、E-C, A-F, H-Gは短6度であり、他は全て長6度である。

以下の音程は7度音程であるが、C-H, F-Eの2つは長7度であり、他は全て短7度である。

以下はいずれも完全8度(1オクターブ)である。

・派生音を含む2音による音程
上記のような幹音のみによる音程であるならば音程の把握も難しいものではない。しかし実際には#やbなどの変化記号が付く事もまたあるのであり、事態はそう単純ではない。このような場合、例えば調号や臨時記号によって音程を形作る音の一方、または両方ともに音程的な変化があるとすれば、以下のような順序で考えるのが分かりやすい。
1.まず2音ともに変化記号をはずして一旦、幹音にもどしてみてその場合の音程を正しく読み取る。
2.そこから再びもとより付されていた変化記号によって、それによって音程がどのように変化するのかを考える。
3.その場合、図1.の図式にしたがって、その変化を追わなければならない
例えば以下の例について考えてみよう。Fis-Hによる音程である。
![]()
a. まずこの場合、度数は4度であって、完全系の音程である事を見てとらねばならない。
b. そして、Fis音の#を一旦取り除き、幹音どうしの状態にする。するとF-Hによる音程という事になるが、このF-Hによる音程は増4度である。
c. 次に再び#を付け戻して考える。#によってFがFisとなり、半音1つ分音程の間隔が狭まった。
d. 図1.の完全系の図式にしたがって、増4度よりも1段階狭い方向へ当てはめれば、この音程は完全となる。
e. したがって、上記の例は完全4度音程である。
以下の例についても考えてみよう。F-Disによる音程である。
![]()
a. この場合、まず音程の度数は6度であり、これは長短系の度数である事がわかる。
b. #を取り除き、F-Dとして考えてみる。このF-Dは長6度である。
c. ここで再び#を付けて考えると、長6度よりも半音1つ分広くなる事がわかる。
d. 図1.にしたがって、”長”より1段階広いのは”増”である。
e. したがって、この音程は増6度である。
以下のような場合はどうであろうか。
![]()
a. まず、この2音がFisisとGisである事に注意する。
b. これは2度音程であって、長短系の音程である。
c. 全ての変化記号や調号を取り除いてみる。するとF-Gとなり、これは長2度である。
d. 続いて#と![]() を付け戻して考えてみる(この場合、調号の#に注意しなければならない)。Fは
を付け戻して考えてみる(この場合、調号の#に注意しなければならない)。Fは![]() が付く事によって半音2つ分上昇し、Gは調号の#によって半音1つ分上昇しているので、双方の上昇分を差し引いて、半音1つ分だけ音程が狭くなっている。
が付く事によって半音2つ分上昇し、Gは調号の#によって半音1つ分上昇しているので、双方の上昇分を差し引いて、半音1つ分だけ音程が狭くなっている。
e. 図1.にしたがえば、長2度よりも1段階狭い音程は短2度という事になるので、この場合の音程は短2度である。
・音程の転回
音程の転回とは、1オクターブ以内のある音程の高い方の音を1オクターブ低くするか、あるいは低い方の音を1オクターブ高くすることによって、別の音程に置き換えるための操作である。このような音程を転回音程という(もとの音程は原音程)。12音技法にあってはいかなる音も、楽器の音域が許す範囲でどのようなオクターブへも転回可能である。しかし12音技法にあっては、転回というよりはむしろ”移高”といったほうが適当であろう。
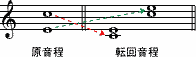
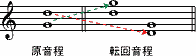
原音程と転回音程とは相互を足し合わせた場合に、ちょうど1オクターブになる関係にある。したがってこの事から、完全、長、短などの音程のタイプと度数は以下に示すように、自分自身をオクターブから差し引いた値として相補的に変換される。
a) 転回された場合の音程の度数の関係。
| 度数の変換 |
| 7度<=>2度 |
| 6度<=>3度 |
| 5度<=>4度 |
| (8度<=>1度) |
b) 転回された場合の音程の種類の関係。
| 音程タイプの変換 |
| 完全<=>完全 |
| 長<=>短 |
| 増<=>減 |
| 重増<=>重減 |
以上、この項目では古典的楽典からの引用として、12音技法における音列の在り方を理解するための一助として有用であろうと思われる音程に関する知識を取り上げてみた。尚、復音程の転回や度数などに関しては、ここでは取り上げなかった。専ら単音程についてであった。それは12音技法においては、いかに復音程的なへだたりのある音程をみせようとも、それはその音の音名において、いかなるオクターブの位置をも取り得る可能性のひとつの表れなのであり、したがって、比較すべき音とのオクターブ内に収まる単音程に還元されるからである。もとより、ここに取り上げた5線記譜法による音程の知識はヨーロッパの伝統的な調性体系のためのものである。それを音列技法に援用する場合、自ずとそぐわない部分もあるのであるが、ともあれ冒頭に記したような理由により、通常はこの慣れ親しんだ記譜法を借用する(実のところ、私が12の半音を扱う場合、一部私独自の記譜法を用いている。その場合、5線譜表ではなく、7線譜表である)。しかし、12音技法の関心は別のところにある。
[ 予備知識編/音程・終了 ] 2003.8.24

| 参考文献 楽典 理論と実習 音楽之友社 新音楽辞典(楽語) 音楽之友社 |