| Appendix-1
Derivation of Eq. (34)
|
|
|
|
| Eq.
(33) is given by
:
|
|
|
f
C (ε) / X (φ) = P (ε) / (X (ε) - X (φ))
|
(1-1)
|
| where,
from Eq. (29),
|
|
|
f
C
(ε) =η (ε) I, II + C I, II (ε) + G (ε)
|
(1-2)
|
| Eq.
(1-1) is changed to be:
|
|
|
f
C
(ε) = P (ε) / (X (ε) / X (φ) - 1) |
(1-3)
|
|
X
(ε) / X (φ) = 1+ P (ε) / fC (ε)
|
|
|
=
( f C (ε) + P (ε) ) / f C (ε)
|
(1-4)
|
|
X
(φ) / X (ε) = f C (ε) / ( f C (ε) + P (ε) ) |
(1-5) |
|
|
|
| Eq.
(17) is given by:
|
|
|
P
(ε) =QM (ε) +AXI (ε) +AXII (ε)
- C
I, II (ε) - η (ε) I, II - G (ε)
|
(1-6)
|
|
|
|
|
From
Eq. (1-2) and Eq. (1-6), we have
|
|
|
f
C (ε) + P (ε) = QM (ε) +AXI (ε) +AXII (ε) |
(1-7)
|
| Eq.
(31) is given by:
|
|
|
QM
(ε) = X (ε) - DX (ε) - AXI (ε)
- AXII (ε)
|
(1-8)
|
| From
Eq.
(1-7) and Eq.
(1-8), we obtain
|
|
|
f
C (ε) + P (ε) |
|
|
=
X (ε) - DX (ε):
denominator of Eq. (1-5) |
(1-9)
|
|
|
|
|
| Appendix-2
Derivation of break-even sales equation corresponding to Solomos’s
problem when the 1st and the 2nd kinds of manufacturing
overhead applied exist |
|
|
| The
two equations, which give the break-even point, are the line-1 given by
Eq. (2-1) and the line-2 given by Eq. (2-2) in Fig. 3. |
|
|
QM / f (ε) + X / (f (ε)
/ tan αXI (ε))=1 |
(2-1) |
|
QM = - AXII (ε) + tan β (ε)
·X
|
(2-2) |
| where |
|
|
tan αXI (ε) = (AXI (ε) - GV (ε)) / X (ε) |
(2-3) |
|
tan β (ε) = ( AXII (ε) + QM (ε))
/ X
(ε) |
(2-4) |
|
f (ε) =f C (ε) - AXII (ε) |
(2-6) |
|
f C (ε) =η (ε) I, II + C I, IIF (ε) + GF
(ε) |
(2-7) |
| |
|
| Eq.
(2-3) has been obtained referring to Eq. (9) in reference (3). In Eq.
(2-3) and in Eq. (2-7), the superscripts V and F
represent variable cost
and fixed cost, respectively. Consequently we have the following
equation: |
|
|
G (ε) = GF (ε) + GV (ε) |
(2-8) |
|
|
|
| Eq.
(2-1) is changed to be |
|
|
QM (ε) + tan αXI (ε) X (ε)=
f (ε) |
(2-9) |
| At
the break-even sales X (φ), Eq.
(2-9) and Eq. (2-2) become: |
|
|
QM (φ) + tan αXI (ε) X (φ)=
f (ε) |
(2-10) |
|
QM (φ) = - AXII (ε)
+ tan β (ε) X (φ)
|
(2-11) |
|
|
|
| Substituting
Eq. (2-11) into Eq. (2-10) gives |
|
|
− AXII (ε) + tan β (ε) X (φ) +
tan αXI (ε) X (φ) = f (ε) |
(2-12) |
| Eq.
(2-12) is changed to be |
|
|
( tan αXI (ε) + tan β (ε) )X (φ) = f (ε) + AXII
(ε)
|
|
|
X (φ) =( f (ε) + AXII (ε) ) / (tan
αXI (ε)
+ tan β (ε) ) |
(2-13) |
|
|
| In
Eq. (2-13) , the numerator and the denominator are: |
|
| f (ε) + AXII
(ε) = f C (ε) |
|
|
= η
I, II (ε) + C I, II (ε) + GF
(ε)
|
(2-14) |
| tan αXI (φ) + tan β (ε) |
|
|
= (AXI (ε) - GV (ε)) / X (ε)
+( AXII (ε) + QM (ε)) / X (ε) |
|
|
= (AXI,II (ε) - GV (ε) + QM
(ε) ) / X (ε) |
(2-15) |
| From
Eq. (31), we have |
|
|
QM
(ε) = X (ε) - DX (ε) - AXI (ε)
- AXII (ε) |
(2-16) |
|
|
|
| Substituting
Eq. (2-16) into Eq. (2-15) gives |
|
|
tan αXI (ε) + tan β (ε) |
|
|
=(X (ε) - DX (ε) - GV (ε) ) / X (ε) |
(2-17) |
| Therefore,
we have |
|
|
X (φ) / X (ε) = (η I, II (ε) + C I, II (ε) +
GF (ε) ) / (X (ε) - DX (ε) - GV (ε) ) |
(2-18) |
|
|
| When
C I, II (ε)= C I, IIF (ε) + C I, IIV
(ε), by similarity between ∆AHF and ∆DHC,
fixed
cost terms always go to numerator and variable cost terms always go to denominator
in Eq. (2-18).
|
|
|
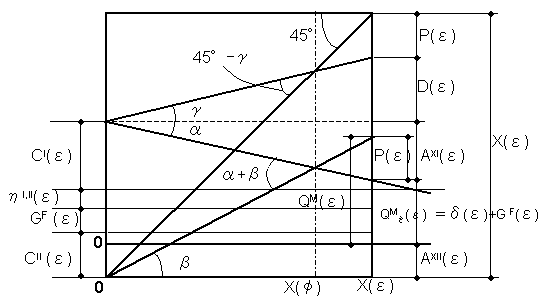
| Appendix-3
Relationship between 45°
break-even chart and managed gross profit chart |
|
| When GV (ε)
=0 and
αXI (ε)
is denoted as α, the
relationship between the 45° break-even chart and the managed gross
profit chart is shown in Fig.
3-1. |
|
|
|
|
Fig.
3-1
Relationship between
45°
break-even chart and managed gross profit chart
|
|
|
|
| When
GV (ε)=0, from Eq. (2-3) and Eq. (2-4) and Eq. (2-17),
we have |
|
|
tan αXI (ε) = AXI (ε) / X (ε) |
(3-1) |
|
tan β (ε) = ( AXII (ε) + QM (ε))
/ X
(ε) |
(3-2) |
|
tan αXI (ε) + tan β (ε)=(X (ε) − DX (ε) ) / X (ε) |
(3-3) |
| From Fig. Appendix-1,
we obtain |
|
|
P(ε)
=
(X (ε) - X(φ))
(
tan αXI (ε) + tan β (ε)) |
(3-4) |
|
P(ε) =
(X (ε) - X(φ))
(X (ε) - DX (ε) )
/ X (ε) |
(3-5) |
|
P(ε) / X (ε) = (1 - X(φ)
/ X (ε)) ·(1- DX (ε)
/ X (ε)
) |
(3-6) |
|
tanγ(ε)
= DX (ε)
/ X (ε) : Variable ratio |
(3-7) |
|
tan αXI (ε) + tan β (ε)
+
tanγ(ε)
=
1 |
(3-8) |
|
P(ε) =
(X (ε) - X(φ))
·
(1-
tan γ(ε)
) |
(3-9) |
|
|
| Appendix-4
45°- gross profit chart |
|
| From
Eq. (19)
in the section of "Outline
of managed gross profit chart theory" , we have |
|
|
P (ε)
= QM
(ε) - Q M
ξ
(ε) |
(4-1) |
|
QM
ξ (ε) = G F (ε) + δ (ε)
|
|
|
= G F (ε) +C (ε) - AX (ε) + η (ε) |
(4-2) |
|
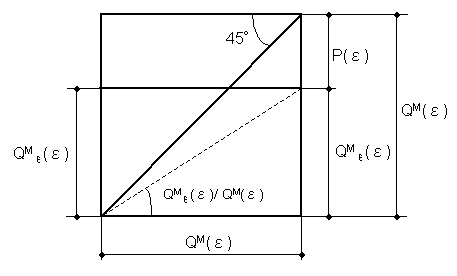
Eq. (4-1) is transformed to
be: |
|
|
QM
(ε)
= P (ε) /(1
- Q M
ξ
(ε) / QM
(ε)) |
(4-3) |
| Eq.
(4-3) means Fig.
4-1. |
|
| |
|
|
|
|
|
Fig.
4-1 45°- gross profit chart |
|
|
|
|
|

