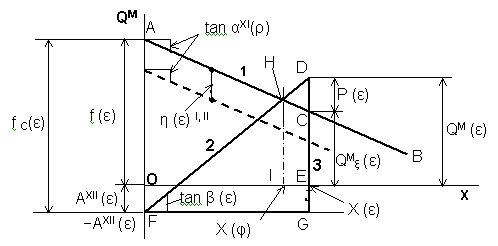
Fig. 3 Managed-gross-profit chart
f C (ε) / X (φ) = P (ε) / (X (ε) - X (φ))
X (φ) / X (ε) = ( η (ε) I, II + C I, II (ε) + G(ε)) / (X (ε) - DX (ε))
| 5-4. Managed-Gross-profit
Chart with both the 1st and the 2nd
kinds of manufacturing overhead applied |
|
| In
general cases, AX (ε) has a combination of AXI
(ε) and AXII (ε). Then the superscripts of 'XI, II'
are defined as follows: |
|
|
AXI, II (ε) = AX (ε) |
|
|
= AXI (ε) + AXII (ε) |
(16) |
|
If
we substitute Eq. (16) into Eq. (7), we obtain the following equation: |
|
|
P (ε) =QM (ε) +AXI (ε) +AXII (ε) - C I, II (ε) - η (ε) I, II - G (ε) |
(17) |
|
Substituting
Eq. (14) into Eq. (17) gives the following equation: |
|
|
P (ε) = QM (ε) +X (ε) · tan αXI (ρ)
+∆ RXI (ρ, ε) + AXII (ε) - C I, II
(ε) - η (ε) I, II - G (ε) |
|
|
= QM (ε) +X (ε) · tan αXI (ρ) - f ρ (ρ, ε) |
(18) |
|
where |
|
|
f ρ (ρ, ε) = η (ε) I,II + C I, II (ε) + G (ε) - AXII (ε) - ∆ RXI (ρ, ε) |
(19) |
| The
marginal condition of QM (ε) in Eq. (18) occurs when P (ε)=0,
under this state QM (ε) is represented as QMξ (ε)
with subscript ξ. Thus QM ξ (ε)
can be given by: |
|
|
QMξ (ε) = f ρ (ρ, ε) - X (ε) · tan αXI (ρ) |
(20) |
|
|
|
IIf
we put P (ε) =0 in Eq. (17), we obtain the following equation: |
|
|
QMξ (ε) = C I, II (ε) - A XI, II (ε) + η I, II (ε) + G (ε) |
(21) |
|
Analogously
we obtain from Eq. (2) the following equation: |
|
|
δ (ε) = C I, II (ε) - AXI , II (ε) + η I, II (ε) |
(22) |
| From Eq.(21) and Eq.(22) we have | |
|
QMξ (ε) =δ (ε) + G (ε) |
(23) |
| From Eq.(21) and Eq.(7) we have | |
|
P (ε) = QM (ε) - QMξ (ε) |
(24) |
| Eq.
(20) can be changed to be: |
|
|
QMξ (ε) / f ρ (ρ, ε) + X (ε) / (f ρ (ρ, ε) / tan αXI (ρ)) = 1 |
(25) |
| Set
up the rectangular coordinates, with the sales X on the horizontal axis
and the managed gross profit QM on
the vertical axis as shown in Fig. 3. If
we observe that Eq. (23) is satisfied at X=X (ε), this shows that
the point (X (ε), QMξ
(ε) ) on the coordinates (X, QM) is located on the
line shown in Eq. (24). The line of Eq. (24) has
f ρ (ρ, ε) of
QM-intercept and tan α XI(ρ)
of slope in Fig. 3. It is noted that the slope of the line is made by
ρ-data. |
|
|
QM / f ρ (ρ, ε) + X / (f ρ (ρ, ε) / tan αXI (ρ)) =1 |
(26) |
| When
the data are on the final statement, or ρ-data → ε-data,
Eq. (24) is written as: |
|
| QM (ε) / f (ε) + X / (f (ε) / tan αXI (ε)) =1 | (27) |
|
f (ε) = η (ε) I, II + C I, II (ε) + G (ε) - AXII (ε) |
(28) |
| If we
introduce the following notation: |
|
|
f C (ε) = η (ε) I, II + C I, II (ε) + G (ε) |
(29) |
|
Eq. (28)
is expressed as |
|
| f (ε) = f C (ε) - AXII (ε) | (30) |
| When
both the 1st and the 2nd kinds of manufacturing overhead applied exist,
QM
(ε) is given by: |
|
|
QM (ε) = X (ε) - DX (ε) - AXI (ε) - AXII (ε) |
(31) |
| QM (X=0) = - AXII (ε) | (32) |
| It is found, from Eq. (29) and Eq. (30), that the line of QM passes through the points (0, - AXII (ε)) and (X (ε), QM (ε)). | |
If we assume, to simplify the discussion, that the 2nd kind of manufacturing overhead applied does not exist, and we replace tan αXI (ε) →αX (ε), f (ε) →f P (ε), ηI (ε) →η (ε), C I (ε) →C F (ε), G (ε) →G F (ε), Eq. (23) becomes the same of Eq. (14) in reference (2). Simultaneously Eq. (29) becomes a line, which passes through the origin and the point (X (ε), QM (ε)). |
|
| As
mentioned above, Table 1, which is the final, income statement including
both the 1st and the 2nd kinds of manufacturing overhead applied, is
charted in Fig. 3. In Fig. 3, the expressions of tan αXI (ρ)
and tan β (ε) are different from those in Fig. 2 in reference
(2). Table 1 is exchangeable to Fig. 3 with each other. When the 2nd
kind of manufacturing overhead applied does not exist, AXII (ε)
is equal to 0 and the point F moves to the origin O. |
|
|
|
|
|
Fig. 3 Managed-gross-profit chart |
|
| In Fig. 3 The intersection point H of the line FD with the line AB is a break-even point under absorption costing. If we denote break-even sales under absorption costing as X (φ), by similarity between ∆AHF and ∆DHC, we obtain the following relation: | |
|
f C (ε) / X (φ) = P (ε) / (X (ε) - X (φ)) |
(33) |
| If we change Eq. (31) by the use of Eq. (27), we have the following break-even sales under absorption costing (referring to Appendix-2): | |
|
X (φ) / X (ε) = ( η (ε) I, II + C I, II (ε) + G(ε)) / (X (ε) - DX (ε)) |
(34) |
| The break-even sales X (φ) in Eq. (32) is a constant number, because X (φ) consists of financial data such as X (ε), DX (ε), C I, II (ε), G (ε) and costs of manufacturing overhead applied in inventories. Consequently, X (φ) is not influenced by arbitrariness of allocation basis of manufacturing overhead. However, break-even sales in direct standard costing is influenced by arbitrariness of allocation basis of manufacturing overhead, if we chart a break-even chart in that costing. This problem will be discussed in another paper by me. | |