| 5-3.
Expression of A |
|
| One departmental manufacturing overhead C (actual cost) is generally close to fixed cost. In general, the manufacturing overhead applied AX (ε) corresponding to C is variable to sales. However there is another case where AX (ε) is close to fixed cost to sales because of the following reason. | |
| In one company, for example, in which products over a limited
production capacity are customarily ordered to outside companies,
the final manufacturing overheads applied per overall company will be close to fixed
costs. This is the special case in which the manufacturing overheads applied
do not follow normal allocation generally expected. |
|
| For this reason, manufacturing overhead applied is termed the ’1st kind of manufacturing overhead applied’, when it is variable to sales, proportional or quasi- proportional, and the kind is shown by the use of the symbol 'I' as in A XI (ε) in this paper. It is also termed the ‘2nd kind of manufacturing overhead applied’, when it is constant or quasi-constant to sales, and the kind is shown by the symbol 'II' as in A XII (ε). The selection of 'I' or 'II' gives no influence to the result of profit calculation and the position of the break-even sales. However, the shape of the managed-gross-profit chart will change a little according to the selection of 'I' or 'II', so there is some significance for the selection in practical accounting. However this will be described later. | |
| As
mentioned in the section 2., the ρ-data were defined as data on forecasted statements
, on the other hand the ε-data were defined
as data on the final statement. Consequently, ρ-data come close to ε-data
as the fiscal period approaches to the year-end to become ρ-data = ε-data at
the year-end. |
|
| By
the above definition, A
XII (ρ) finally reaches to A
XII (ε)
at the year-end regardless of the amount of X (ε) . Although A
XI (ε)
is quasi-proportional to increase and decrease of X (ε), in fact, A
XI
is a non-linear function with respect to X (ε) by the following reasons. |
|
| (1)
When
manufacturing overhead applied is determined, for
example, by multiplying standard overhead
rate by allowable standard job hours, the hours
are not exactly proportional to actual sales. |
|
| (2)
If allocation basis of AX is predetermined
in such a manner that AX is proportionate to X (ε) ,
the amount of AX for goods manufactured depends upon state of human
mind because of human activity. For example, if computer utility rate is
predetermined internally by utility hours based on company's past experience, it
sometimes happens that resulting actual utility hours decrease because
users make efforts not to use computers for cost saving. |
|
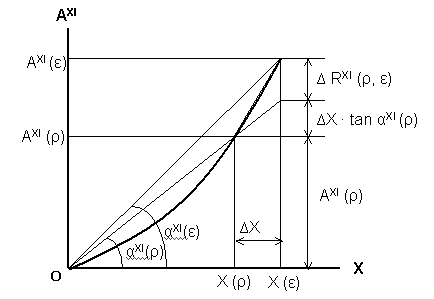
| Charting Eq. (7) is the problem to be resolved. For the purpose, QM and AX should be expressed as functions of the variable X. When we consider that AXI (ε) is a nonlinear function of X (ε) , we attempt to express A XI (ε) with the use of both A XI (ρ) and an incremental sales from X (ρ). | |
| The resulting
equation for A
XI (ε) is expressed, by referring to Fig. 2, which is: |
|
|
AXI (ε) = AXI (ρ) + ∆X · tan αXI (ρ) +∆ RXI (ρ, ε) |
(8) |
| where |
|
| ∆X =X (ε) - X (ρ) | (9) |
| tan αXI (ε) = AXI (ε) / X (ε) | (10) |
| tan αXI (ρ) = AXI (ρ) / X (ρ) | (11) |
| ∆ RXI (ρ, ε)=X (ε) (tan αXI (ε) - tan αXI (ρ)) | (12) |
| In Eq. (8) the following equation is satisfied. | |
|
AXI (ρ) + ∆X tan αXI (ρ) |
|
|
=
AXI (ρ) + (X (ε)
-
X (ρ))
AXI (ρ)
/ X (ρ) |
|
| = X (ε) tanαXI (ρ) | (13) |
| Consequently Eq.(8) is also expressed as: | |
|
AXI (ε) = X (ε) tan αXI (ρ)+∆ RXI (ρ, ε) |
(14) |
| The
meaning of Eq. (8) is that the more approximate value to AXI (ε)
is AXI (ρ) + ∆X · tan αXI (ρ),
and its
error is ∆ R XI (ρ, ε), when AXI (ρ) is given as
an approximate value of AXI (ε) |
|

Fig.
2 Expression of AXI (ε) by AXI (ρ) and ∆X
| In
the special case where we only deal with a forecasted or a final statement
individually, ρ-data is equal to ε-data, therefore ∆ RXI (ρ,
ε)=0 from Eq. (12). When sales X are directly proportional to manufacturing
overhead applied AXI, the following equation is obtained: |
|
|
AXI
(ρ) / AXI (ρ) = AXI (ε) / AXI (ε) |
(15) |
| In that
case we have ∆ RXI (ρ, ε)=0
from Eq. (12). |
|
| The value of (tan αXI (ε) - tan αXI (ρ)) approaches zero and the value of ∆RXI (ρ, ε) becomes small, when the ratio AXI (ε) / X (ε) is almost constant regardless of the amount of X (ε) as in general cases. If we modify the ρ-data to the ε-data with approach to the year-end, finally we have ∆ RXI (ρ, ε)=0. | |