§3 Examination of the Keynesian Multiplier Effect Theory
DCE Hayashi, Yuichiro
| Keynes' principle of effective demand based on the the Keynesian multiplier effect is mathematically wrong. | ||
| The Keynesian multiplier effect doesn't exist. | ||
|
|
||
| December 2003 | ||
| 1. Derivation of the Keynesian multiplier effect | ||
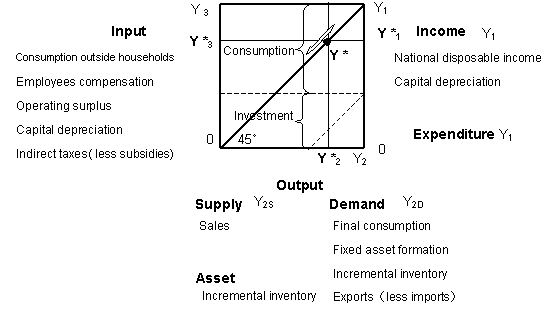
| In order to avoid complications on symbols, we shall consider a closed economy. Let Y be the gross value added (GVA) in the national economic accounting, and ' * ' be the equilibrium point , or the "Keynesian Cross". | ||
| Furthermore, the following notations are defined: Y3 = the gross value added; Y2 = demand( final products from the standpoint of customers) or supply( those from producers); Y1 = gross income( the value to which the GVA is distributed to firms, households and a government). | ||
| In the author's theory, he insists on the existence of the break-even chart, between production and demand in the national economic accounting, which is to be a foundation for theoretically analyzing the economy. Therefore, he adds the following definitions: Y3 = input in economic activity ( costs and profit in final products); Y2=output in economic activity ( final products with stocks). Y1= both a broken-down value and the residual one, from the value Y2, which are carried into Y3 as its generation resources. | ||
| The relationship between the notations shown in Fig. 3-1 is assured by the principle of equivalent of three aspects. | ||
|
||
| Fig. 3-1 Definition of three aspects Y 1, Y 2 and Y 3 | ||
| The Keynesian consumption function is expressed as follows: | ||
| C 2 = a A + a K ( Y 1 -T1 ) | ||
|
= a B + a K Y1 |
(3-1) | |
| where | ||
| C2: Private consumption | ||
| T 1: Taxes | ||
| a A : Consumption at Y1 -T1 =0 | ||
| a K: Marginal propensity to consume( MPC) | ||
| a B= a A - a K T1: a B is independent of consumption. | ||
| Demand Y2D is expressed as follows: | ||
|
Y2D = C2 + I 2 + NX 2 + G2 |
(3-2) | |
| where | ||
| I 2= I 2 (r) : Private investment is a function of interest rate ' r ' . Rate r is assumed constant, so private investment I 2 is independent of private consumption. | ||
| G2 : Government expenditure is determined by government will, so G2 is assumed independent of private consumption. | ||
| NX 2 : Net exports( exports − imports) are assumed independent of private consumption. | ||
| We will adopt the following assumptions: | ||
| Assumption 1: Consumption C 2 is a linear function of variable Y 1, so that the consumption function can be defined for Y 1. | ||
| Assumption 2: T1 , I 2 , NX 2 and G 2 are independent variables of C 2. | ||
| Assumption 3: The incremental inventory is included in I 2. | ||
| In addition, I add the following assumptions in order to clarify the matters in question, highlighted in this problem. | ||
| Assumption 4: In this problem, operating surplus P is kept constant. This assumption has been added to relate §1 to §2. | ||
| Furthermore, the independence of I2 andNX2 is expressed as the following assumption: | ||
| Assumption 5: I2 and NX2 are constant with respect to Y2, that is, ΔI2 + ΔNX2 = 0 or ΔI2 = ΔNX2 = 0, so that G2 is a variable which doesn't have a functional relation to Y2. | ||
| Assumption 6: For simplicity of notations, it is assumed that incremental government consumption is not included in incremental government expenditure. | ||
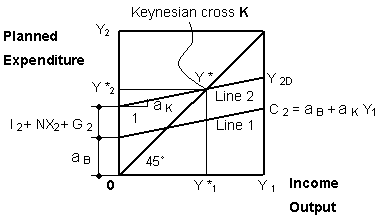
| Eq. (3-1) and Eq. (3-2) are shown in Fig. 3-2. Line 1 is the consumption function Eq. (3-1). Line 2 shows Eq. (3-2), and indicates the relationship between income and planned expenditure. The 45° line shows the relationship between income and actual expenditure( = supply Y2S). Cross point K is the 'Keynesian cross'. At this point the actual demand and supply are determined. | ||
|
|
||
| Fig.3- 2 Consumption function | ||
| At the Keynesian cross K, the following holds: | ||
|
C *2 = a B + a K Y *1 |
(3-3) | |
|
Y *2D = C *2 + I *2+ NX *2 + G *2 |
(3-4) | |
| Planned demand Y 2D approaches actual demand Y *2D (= actual supply Y *2S), that is: | ||
|
Y *2S = Y *2D |
(3-5) | |
| Substituting Eq. (3-3) and Eq. (3-4) into Eq. (3-5) gives: | ||
| Y *2S = a K Y *1 + a B + I *2+ NX *2 + G *2 | (3-6) | |
| At the Keynesian cross we have: | ||
|
Y *2S = Y *2D = Y *1 =Y * |
(3-7) | |
| Substituting Eq. (3-7) into Eq. (3-6) yields: | ||
| Y * = a K Y * + a B + I *2+ NX *2 + G *2 | (3-8) | |
| Therefore, we obtain: | ||
| Y * = ( a B + I *2 + NX *2 + G *2 ) / (1 - a K) | (3-9) | |
| If we suppose that in Eq. (3-4), when Y *2D increases as much as Δ Y, C *2 and G *2 increase as much as Δ C 2 and Δ G 2 respectively, and that I *2 and NX *2 remains unchanged, we obtain: | ||
| Y *2D +Δ Y 2 | ||
| = (C *2 + Δ C 2 ) + I *2 + NX *2 + ( G *2 + Δ G 2) | (3-10) | |
| From Eq. (3-4) and Eq. (3-10), we obtain: | ||
| ΔY2 = ΔC 2 + ΔG2 | (3-11) | |
| At the Keynesian cross we have, from Eq. (3-3): | ||
| ΔC2 = a K ΔY1 | (3-12) | |
| Substituting Eq. (3-12) into Eq. (3-11) gives: | ||
| ΔY2 = Δ Y 1 = Δ Y = Δ G 2 / (1 - a K) | (3-13-1) | |
| ΔG2 = (1 - a K) Δ Y1 | (3-13-2) | |
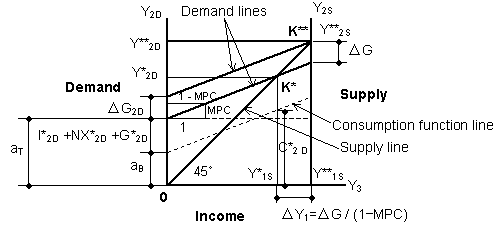
| As shown in Fig. 3-3, incremental demand Δ G2 gives multiplier effect Δ G2 / (1 − aK) for gross income Y1. (Ref.: N.G.Mankkiw, "Macroeconomics", p.265, fifth edition, Worth Publishers, 2002.) | ||
|
|
||
| Fig. 3-3 Keynesian multiplier effect | ||
| The multiplier effect theory appears to have no errors. What is the difference between MPC (=a K ) and variable cost ratio a V in the input-output table chart shown in §1 ? | ||
|
2. Meaning of the multiplier effect |
||
| Before re-examining the Keynesian multiplier effect, we will consider when the multiplier effect factor 1 / (1 - a) appears in economics. | ||
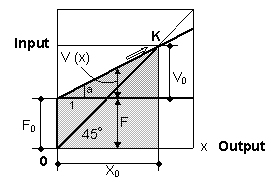
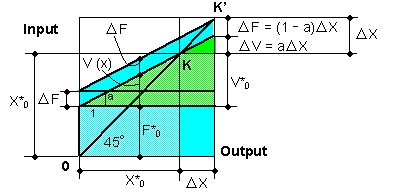
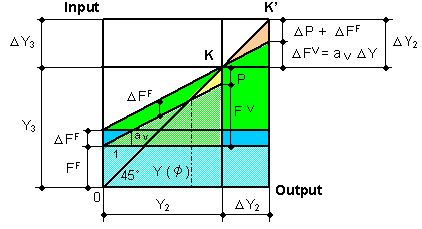
| The shape of factor 1 / (1 - a) appears in the case shown in Fig. 3-4. The horizontal axis x shows products or output, not including profit value in a firm. The vertical axis shows input or costs( injected energy) without profit value in order to produce x. The costs consist of a fixed cost F and a variable cost V (x). Fixed cost F means that it is not affected by a change in output x. In Fig. 3-4, we want to get output x where inputs F + V (x) = output x. We can find such a point at the cross point K between the 45°line and cost line F+ V (x). At point K we define the notation, X 0 = F 0 + V 0. | ||
|
|
||
|
Fig. 3-4 Relationship between output and input |
||
| The above problem can be solved as follows: | ||
|
x (output) = F (input) + V (x) (input) |
(3-14) | |
| At the point where output = inputs, we denote x = X 0 and V (X 0) = V 0 . Then we have: | ||
|
F0 = X 0 - V 0 |
(3-15) | |
|
1 / F0 = 1 / ( X 0 - V 0 ) |
||
| X 0 / F0 = 1 / ( 1 - V 0 / X0 ) | ||
| X 0 = F0 / ( 1 - a ), where a = V 0 / X 0 | (3-16) | |
| X 0 (output) can be expressed in 3 ways: | ||
| (1) X 0 (total input = output) | ||
| (2) F 0 (input) + V 0 (input) | ||
| (3) ( X 0 - V0 ) / ( 1 - a ) = F0 / (1 - a), where a = V 0 / X 0 | ||
| The above 3 values are equal to each other. The third way is verified as follows: | ||
| F 0 / ( 1 - a) = F 0 / ( 1 - V 0 / X 0) | ||
| = X 0 F 0 / ( X 0 - V 0 ) | ||
| = X 0 (total input) | ||
| Then, we have: | ||
| F 0 / ( 1 - a) = F 0 + V 0 = X 0 | (3-17) | |
| The meaning of F 0 / ( 1 - a) is that output X 0 can be expressed as F0 / ( 1 - a) using the two fixed terms, F 0 and ' a ', when input V (x ) is continuously provided and sales V (x ) are continuously realized. | ||
| At point K in Fig. 3-4, the symbol '*' is added to the previously defined notations. When X*0 becomes X*0 + Δ X , we will consider where point K moves. From Eq. (3-14), we have: | ||
|
X *0 = F *0 + V *0 |
(3-18) | |
|
X *0 + Δ X = F *0 + Δ F + V *0 + Δ V |
(3-19) | |
| Then we have: | ||
|
Δ X = Δ F + Δ V |
(3-20) | |
| Case-A | ||
| When Δ F = 0 at point K, F is equal to a constant( completely fixed value) , we obtain: | ||
| Δ X (output) = Δ V (input) | (3-21) | |
| Since V / X = a (≠0, constant), the following holds: | ||
|
Δ V = a Δ X |
(3-22) | |
| The solution of Eq. (3-21) and Eq. (3-22) is Δ V = Δ X = 0, so that point K can not move by the constraint, input =output, when Δ F = 0. The meaning of Δ F = 0 is that the new input energy( costs) in the fixed costs is not provided. In order for point K to move, Δ F should be provided, or the condition Δ F = 0 should be removed. | ||
| Case-B | ||
| When point K can move to K', we have, from Eq. (3-20): | ||
| Δ X ( output) = Δ F (input) + Δ V (input) | (3-23) | |
| Eq. (3-23) is shown in Fig. 3-5. Fig. 3-5 shows that point K moves on the 45°line keeping output = input. In this case, Δ F means that Δ F is a variable, and the amount of Δ F is not affected by an output change. | ||
|
|
||
| Fig. 3-5 | ||
| We denote outputs of goods as X . We suppose that the goods are produced spending fixed( independent) inputs F and variable inputs V for a change of X, and a = V / X= a constant. As mentioned above, the equation X = F / ( 1 - a ) appears when outputs X = inputs ( F + V), so F / ( 1 - a ) is another expression of X. Notice that the equation X = F / ( 1 - a ) holds when F is also a variable. The reason is that the equation shows the component ratio between X, F and V, whether F or V is a variable or not. | ||
|
3. Meaning of the Keynesian multiplier effect |
||
| Let's consider the meaning of the Keynesian multiplier effect. Eq. (3-11) and Eq. (3-12) are written again below. | ||
| Δ Y 2 = Δ C 2 + Δ G 2 | (3-11) | |
| Δ C 2 = a K Δ Y 1 | (3-12) | |
| The amount of MPC (= a K ) is about 0.6 to 0.7. Variable cost ratio a V is nearly equal to the economic growth rate, so the amount of a V is roughly within ±0.05. Hence, Δ C 2 is not a part of the incremental input (cost) but a part of the incremental whole output Y 2( aggregate demand or supply). Δ G 2 is, as a matter of course, a part of output. Thus, Eq. (3-11) shows that the whole ΔY 2 consists of both parts Δ C 2 and Δ G 2. We obtain Δ C 2 / Δ Y 2 = a K from Eq. (3-1), so Δ C 2 = a K ·Δ Y 2 = a K ·Δ Y 1 . Therefore, only the following situation is allowed on the Keynesian cross: | ||
| Situation; If Δ C 2 / Δ Y 1 = a K, then Δ G 2 = Δ Y 1 (1 - a K) = Δ Y 2 (1 - a K). | ||
| If we suppose Δ Y 2 = Δ G 2 and substitute this into the above equation, we get 1 = 1 − a K. This is obviously wrong. | ||
| The Keynesians claim that the following is possible under the condition Δ Y3 = Δ Y2 in firms: Δ Y2 = Δ G < Δ Y1 = Δ G / (1 - a K) = Δ G + a K Δ G / (1 - a K); We reserve Δ G; Δ Y '2 = a K Δ G / (1 - a K) ; Δ Y '2 < Δ Y '1 = a K Δ G / (1 - a K)2 ; Δ Y ''2 = a K Δ G / (1 - a K)2 ; Δ Y ''2 < Δ Y ''1 = a K Δ G / (1 - a K)3· · · Δ Y '1→∞. If this cycle is right, a perpetually expanding economic motion holds by the first Δ G. This is illogical. | ||
| According to the input-output table chart in §1, the right side of Eq. (3-11) must be input, because the left side term Δ Y 2 is output( supply). However, both sides of Eq. (3-11) are incremental outputs for firms. | ||
| In order to resolve the Keynesian multiplier effect problem, we have to investigate the relationship between an incremental whole and its incremental parts. | ||
| 4. Growth rate of output which has 2 classes of goods | ||
| Suppose that there is, in a nation, total fruit output W ( measured in monetary value), which consists of orange quantity A and apple quantity B per annum. The monetary value is supposed to be equal to labor costs. Time ( year unit) is denoted as ' t '. The symbol (t) in the functional expression f (t) is omitted. Notations are added as follows: | ||
| a = A / W : Ratio of A to W | ||
| b = B / W : Ratio of B to W | ||
| w = d W / d t : Growth rate of W | ||
| w a = d A / d t : Growth rate of A | ||
| w b = d B / d t : Growth rate of B | ||
| It is assumed that: | ||
| Assumption I: there is no inflation and deflation; | ||
| Assumption II: W is growing every year, so w ≠0 and Δ W exists; | ||
| Assumption III: the increase of A is independent of the increase in B. The reason is that the person who likes orange does not like apple and vice versa, so each increase will always occur independently of each other. | ||
| We have the following equations: | ||
| W = A + B | (3-24) | |
| Δ W = Δ A + Δ B | (3-25) | |
| w = w a + w b | (3-26) | |
| a + b = 1 | (3-27) | |
| Δ a + Δ b = 0 | (3-28) | |
| Since A = a · W and B = b · W, we have: | ||
| Δ A = a · Δ W + Δ a · W | (3-29) | |
| Δ B = b · Δ W + Δ b · W | (3-30) | |
| When t = t n, we define notations as follows: | ||
| W ( t n ) = W n | ||
| W ( t n+1 ) = W n+1 | ||
| Δ W = W n+1 − W n | (3-31) | |
| These notations are used for A, B, w, w b, w a, a, and b. | ||
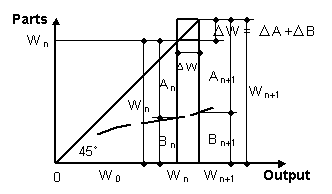
| From these relations we have the following charts: | ||
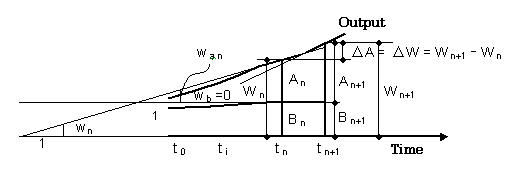
| CASE-A : w b = 0 | ||
| When w b consistently equals 0, the statistic, time series ( year unit) fruit outputs are shown in Fig. 3-5. From Fig. 3-5 we easily obtain: | ||
| Δ W = Δ A | (3-32) | |
| w a = w | (3-33) | |
| The above results show that incremental part Δ A equals incremental whole Δ W, so the growth rate of A ( t ) is the same as that of W ( t ). | ||
|
|
||
| Fig. 3-5 Relationship between Δ W and Δ A when w b = 0 | ||
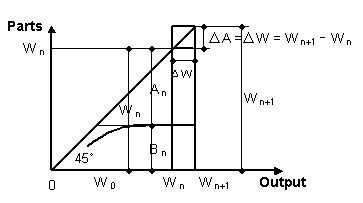
| We set up the rectangular coordinates where whole output W is the horizontal axis, and the sum of the parts in the whole is the vertical axis. Thus, the data W0 ( = 0 ), W 1, · · W i· ·W n, W n+1, are put on the horizontal axis, so that we have Fig. 3-6. The order of data W i ( t i ) on the horizontal axis is, as a matter of course, changeable. | ||
|
|
||
|
Fig. 3-6 Chart with rearranged data when w b = 0 |
||
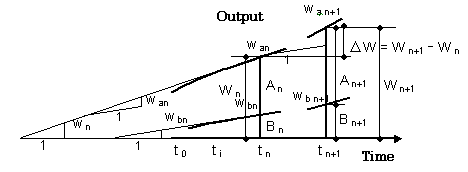
| CASE-B : w a ≠ 0 and w b ≠ 0 | ||
| When w a ≠ 0 and w b ≠ 0, in a similar manner we have Fig 3-7 and Fig.3-8. | ||
|
|
||
|
Fig. 3-7 Relationships between the terms when w a ≠ 0 and w b ≠ 0 |
||
|
|
||
| Fig. 3-8 Chart with rearranged data when w a ≠ 0 and w b ≠ 0 | ||
| In Case-B, Δ W is a function of the two terms, Δ A and Δ B, so Δ W cannot be determined by the single term Δ A or Δ B. In this case, the effect of parts Δ A and Δ B on incremental whole Δ W will be considered. | ||
| Adding Eq. (3-29) and (3-30), we have: | ||
| Δ A + Δ B = ( a + b ) Δ W + ( Δ a + Δ b ) W | (3-34) | |
| From Eq. (3-27) and Eq. (3-28), we have: | ||
| Δ A + Δ B = Δ W | (3-35) | |
| It is a logical conclusion that the total changes in the part equal the change in the whole. | ||
| Through both cases, it is found that the rate of change in the sum of parts A + B is the same as that of whole W, which is the growth rate of W itself. Assumption III has not been used, and therefore it is unrelated to this problem. | ||
| 5. Re-examination of the Keynesian multiplier effect | ||
| Eq. (6) and Eq. (11) are shown again below: | ||
| Y *2 = [1] + [2] | (3-36) | |
| [1] = [a B + a K Y *1] = C *2 | ||
| [2] = [ I *2 + NX *2+ G *2 ] | ||
| Δ Y 2 = Δ C 2 + Δ G 2 | (3-11) | |
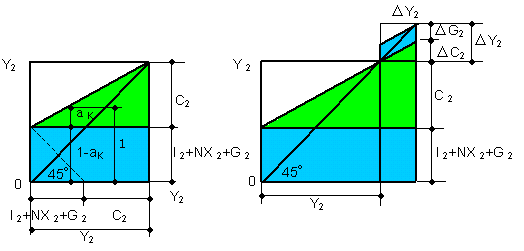
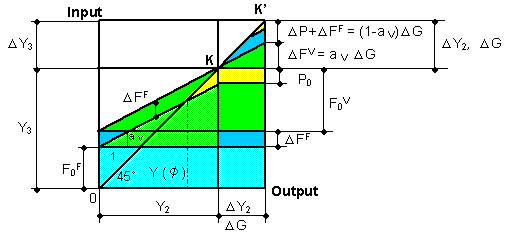
| Both term [1] and term [2] are parts of final demand, according to the input-output table. Therefore, each term is merely a part of whole output Y *2. According to the Keynesian theory, Term [1] is a variable, because we have Δ C 2= a K Δ Y 1= a K Δ Y 2. It is assumed that I *2 + NX* 2 is a constant( completely fixed value), because we have Eq. (3-11). Δ G 2 is a variable because we have the incremental value Δ G 2 in this analysis. | ||
| It should be noted that both Δ C 2 and Δ G 2 are outputs when we consider the production aspect. In the Keynesian theory, it is assumed that Δ G 2 is independent of Δ Y. This means that Δ G 2 is not affected by a change in Y 2. As we do not take into consideration, right now, input energy ( labor, profit) in this analysis, the current economic model is shown in Fig. 3-9. | ||
|
|
||
|
(a) (b) |
||
| Fig. 3-9 Keynesian model | ||
| Ratio a K ( MPC ) is originally defined in such a manner that C 2 is a ratio of consumption product to total product Y2. In Fig. 3-9 (a), a K (= C2 / (C2+constant)) is not obviously constant but a function of C2 ( = f(Y2) ). The Keynesian model holds only when a K is constant. Therefore, the model shown in Fig. 3-9 is incorrect. | ||
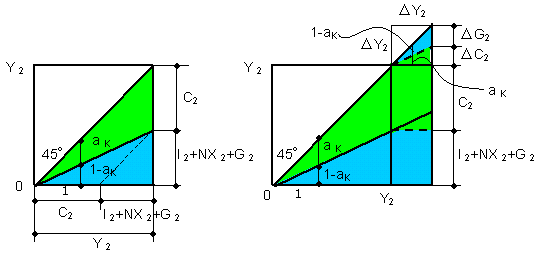
| Fig. 3-9 should be corrected as shown in Fig. 3-10, in which a B in Eq. (3-1) has been neglected. In Fig. 3-10, an error is included intentionally. The error is Eq. (13-1) itself. Eq. (3-11) should correctly be written as: | ||
| Δ Y 2 = Δ C 2 + Δ I2 + Δ NX2 + Δ G 2 | (3-37) | |
| Δ Y = Δ C + Δ I + Δ NX + Δ G | (3-37-1) | |
| Eq. (3-37-1) is the equation where only the subscript 2 has been omitted. We cannot assume that I2 + NX2 is constant, because the same problem, included in Fig. 3-9, occurs again. Ratio a K is originally defined between C2 and Y2 (= C2 + I2 + NX2 + G2). We must preserve the condition where a K is constant and a K is the ratio of C2 to Y 2. However, a K is used between Δ C2 and Δ G2 in increment Δ Y 2. Consequently, Δ G 2 in Fig.3- 9 (b) should be replaced by Δ I2 + Δ NX2 + Δ G2. | ||
|
|
||
|
(a) (b) |
||
| Fig. 3-10 Corrected Keynesian model-1 | ||
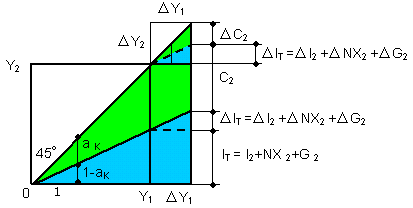
| After these corrections are made, we obtain Fig. 3-11. | ||
|
|
||
|
Fig. 3-11 Corrected Keynesian multiplier effect model |
||
| Δ G 2 in Eq. (3-11) has been replaced by Δ I2 + Δ NX2 + Δ G 2. In this figure, Δ G 2 should be expressed, due to statistical result, as: | ||
| Δ G 2 = (1 - a K) Δ Y2 G 2 / ( I2 + NX2 + G2 ) | (3-38) | |
| The expression of Eq. (3-38) means that each incremental expenditure in the right side of Eq. (3-37), derived from Eq. (3-2), should be expressed by using each 'marginal propensity to expend' for the gross income Y1. | ||
| The amount of supply Y2, that is GDP or gross value added Y2, is equal to gross value added Y3, measured by input energy in firms, or gross income Y1 measured by gross income, then we have ΔY2 = Δ Y3= Δ Y1. Hence, each component such as Δ G 2 in Eq. (3-37) has an incremental gross value added which is equivalent to the component's product value itself. If we regard Δ G 2 in Eq. (3-37) as a summation of unit contracts which belong to Δ G 2, Δ G 2 is a part of the total firms' output in the national economic accounts. Thus, each component such as Δ G should be treated individually as the incremental whole ΔY2 in Fig. 3-11. These explanations are the logical result of the Keynesian multiplier effect model. | ||
| 6. Explanation by an example | ||
| This logic will be explained through the cost of a party. There are 4 dishes available at the party, Consumption, Investment, Net export, and Government expenditure. The cost of 100 servings of each dish is denoted as C0, I0, NX0 and G0, respectively. The total cost of all dishes is denoted as Y0, so Y0= C0+ I0 + NX0 + G0. Furthermore, we define aC=C0 / Y0, aI=I0 / Y0, aNX=NX0 / Y0 and aG=G0 / Y0. Obviously, aC + aI + aNX + aG = 1. It is assumed that these coefficients aC, aI , aNX and aG have been gotten through statistical observations of normal cooking costs for 100 persons. | ||
| The number of party guests has been hastily changed to 110 people, and the additional cost is Δ G. The total cost and the cost of each dish are calculated in the following: | ||
| (1) when only the G-dishes are additionally ordered, the total cost is calculated by Y0+ Δ Y=Y0+ Δ G, .Δ Y=Δ G; | ||
| (2) when all 4 kinds of dishes are ordered, the total cost is calculated by Y0+ΔY = Y0+ Δ G, Δ Y = Δ G, Δ Y = Δ C + Δ I + Δ NX + Δ G' = (aC + aI + aNX + aG) Δ Y, where Δ C = aCΔY, Δ I = aIΔY, Δ NX = aNXΔ Y, Δ G' = aGΔY. | ||
| In case (1), we only get Δ Y=Δ G. This case corresponds to the above-mentioned description. | ||
| In case (2), we can easily find the following equations: Δ Y= Δ G = (Δ I + Δ NX + Δ G') / (1 - aC)= (Δ I + Δ NX) / (1 - aC - aG ) = Δ G' / (1 - aC - aI - aNX) and so forth. The first equation Δ Y= Δ G= (Δ I + Δ NX + Δ G') / (1 - aC) is equivalent to the equation Δ G - Δ C = Δ I + Δ NX + Δ G', that is Δ G = Δ C + Δ I + Δ NX + Δ G'. These equations merely show Δ Y=Δ G, Δ C = aCΔ Y, Δ I = aIΔ I, aC = C0 / Y0 and so forth. | ||
| From each case, we have Y0+Δ Y = Y0+ Δ G, Y0= C0+ I0 + NX0 + G0, C0 = aC Y0, I0 = aI Y0 and so forth. The Consumption-dish coefficient aC always exists and is used in this process. The incremental cost Δ G is equal to the increment of the total Y0, that is Δ Y. | ||
| 7. Error points in the Keynesian multiplier model | ||
| We will consider again points where the Keynesians made errors. The errors are found in Fig.3- 9, Fig. 3-10 and Fig. 3-11. Eq. (37-1) is changed to: | ||
| Δ Y = Δ G / (1 - aK) + ( Δ I + Δ NX) / (1 - aK) | (3-39) | |
| The Keynesian model's equation is as follows: | ||
| Δ Y = Δ G / (1 - aK) | (3-13-1) | |
| (1) The transformation from Eq. (3-39) to Eq. (3-13-1) is equivalent to making the assumption: Δ I +Δ NX = 0. This assumption means that both C and G are affected by a change in Y, and ( I + NX) is not affected. However, private investment I is largely affected by a change in Y. This is the Keynesian model's first error. | ||
| (2) As mentioned above, Δ G is affected by a change in Y. Then, Δ G should take the shape of Δ C as shown in Fig. 3-10(b). However, G is treated like (I + NX) in Fig. 3-9(b). This is the Keynesian model's second error. | ||
| (3) Eq. (3-13-1) is equivalent to Eq. (3-11) where subscript 2 has been omitted. | ||
| Δ Y = Δ C+ Δ G | (3-11) | |
| If Eq. (3-11) was correct, statistical results obtained through the observation of (Y - C ) should agree with those obtained through the observation of G. However, the consumption function is defined in such a manner as to satisfy Eq. (37-1) . This is the Keynesian model's third error. | ||
| (4) As mentioned above, Δ G should be treated as the incremental total Δ Y in Fig.3-11. However, Δ G is regarded as a part of Δ Y as well as Δ C in Fig. 3-3. This is the Keynesian model's fourth error. | ||
| (5) According to the national economic accounts, the incremental gross value added, Δ Y, should become the same value when it is measured between aspects, Y1, Y2 and Y3 . The total increment Δ Y2 is represented as Δ Y2 =Δ G 2. On the other hand, in the Keynesian model, Δ Y2 = Δ C 2(=a K Δ Y1)+ Δ G 2. This is a contradiction. This is the Keynesian model's fifth error. With regard to this problem, someone may say that Δ C in the equation will be produced at some point in the future. However, this is wrong. The incremental consumption Δ C by Δ G is not necessarily assured in the future. Because firms profits and wages have a competing relationship (as explained in §4 in 'Management Accounting'), there is a possibility that Δ G is used only for the recovery of the firms' losses, so consumer confidence does not revive in a depression. | ||
| In conclusion, the Keynesian multiplier effect theory is mathematically wrong. Output Y 2 should be related to input Y 3 in firms in the input-output table or gross income Y1 in the national economic accounts. | ||
| 8. Effect of government expenditure | ||
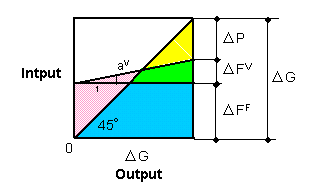
| As the Keynesian multiplier effect with MPC has been denied, the effect of incremental government expenditure Δ G will be examined by using variable cost ratio a V. Fig.3- 12 is the chart where notation X (found in Fig. 2-8 in in §2) has changed to GDP Y. In this chart, a V = FV / Y, and Δ Y = Δ P +Δ FV + Δ FF. | ||
|
|
||
| Fig. 3-12 Chart from Fig. 2-8 in §2 | ||
| Δ G should be expressed as shown in Fig. 3-13 and Fig. 3-14. | ||
|
|
||
|
|
||
|
Fig. 3-14 Relationship between Components in Δ G |
||
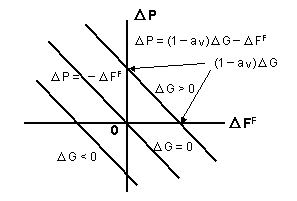
| From Fig. 3-14, we have: | ||
| Δ P = Δ G - Δ FF - Δ FV | ||
| = (1 - a V) Δ G - Δ FF | (3-40) | |
| Fig. 3-2 in §5, 'Accounting' is verified by Eq. (3-40). When Δ FF = P0 and Δ G = Δ FV + Δ FF = Δ FV + P0, we obtain, Δ P = Δ FV + P0 - P0 - Δ FV = 0. | ||
| From Eq. (41), the relationships between Δ P, Δ FF and ΔG are obtained as shown in Fig. 3-15. | ||
|
|
||
|
Fig. 3-15 Relationship between Δ P and Δ FF |
||
| Ratio a V is not MPC but a V = FV / Y or variable cost ratio. Variable cost FV is a part of supply Y. Consequently, Ratio a V is a small figure, then 1 / (1 - a V) nearly equals 1 + a V. In Fig. 3-13, the allocation of Δ P and Δ FF to Δ G depends upon both entrepreneurs' will and external evaluation. | ||
| Let's regard Δ G as a minimum unit in an economic society, for example, a contract including buying and selling of a product. As a matter of course, each unit's ratio a V is different from the other. The shape of each unit's profit chart and the whole is the same. At the last stage, we find the profit chart connecting the whole with its units. If we add an incremental financial asset and liability for each contract, we will be able to express the whole economic flow from each unit to the whole of the units. | ||
| This theory, formulated by me, is the fundamental theory derived from the national economic accounts, and so applies to both the short run and the long run economy. | ||
| 9. Review | ||
| From the national economic accounts, we have the following equations: | ||
|
Y2 = C 2 + I 2 + NX 2 + G 2 |
(3-R1) | |
|
Y2 = Y1 |
(3-R2) | |
|
ΔY2 =Δ C 2 + ΔI 2 + ΔNX 2 + ΔG 2 |
(3-R3) | |
|
ΔY2 =Δ Y1 |
(3-R4) | |
| where Y1 = income and Y2 = goods or services. | ||
| From Eq. (3-R3), we have | ||
|
Δ C 2 / ΔY2 + ΔI 2 / ΔY2+ ΔNX 2 / ΔY2+ ΔG 2 / ΔY2 = 1 |
(3-R5) | |
Substituting Eq. (3-R4) into Eq. (3-R5) gives: |
||
|
Δ C 2 / ΔY1 + ΔI 2 / ΔY1+ ΔNX 2 / ΔY1+ ΔG 2 / ΔY1 = 1 |
(3-R6) | |
| We define the following notations, which are statistically observed,: | ||
aK = Δ C 2 / ΔY1, aI = Δ I 2 / Δ Y1, aNX = ΔNX 2 / ΔY1 and aG = ΔG 2 / ΔY1, where all the coefficients are constant. Some coefficients are allowed to be zero at a closed time interval in Y2. The coefficient aK is the same as MPC. |
||
| Between these coefficients, from Eq. (3-R6), we have the following: | ||
|
aK + aI + aNX + aG =1 |
(3-R7) | |
| Eq. (3-6) can be transformed to: | ||
|
ΔY1 = (ΔI 2 + ΔNX 2 + ΔG 2) / (1 - aK) |
(3-R8) | |
|
ΔY1 = ΔG 2 / (1 - aK - aI - aNX ) |
(3-R9) | |
| Eq. (3-R5), Eq. (3-R6), Eq. (3-R8) and Eq. (3-R9) are equivalent to each other under Eq. (3-R4) with the above notations | ||
| We can't assume that ΔI 2 + ΔNX 2= 0, because private investment I is largely affected by a change in Y, so (aI + aNX) is not zero in the real economy. If we adopt the assumption ΔI 2 + ΔNX 2 = 0, aK will become a nonlinear function of Y1. | ||
| We may momentarily have Eq. (3-11) at ΔI 2 + ΔNX2= 0, and we have Eq. (3-R3) for such a time period that MPC is determined, because ΔI2 and ΔNX2 exist for the period. | ||
| The differences between the products C 2, I 2 , NX2 and G2 depend on mainly in purchasers and product life. Each product is produced by using (expending) Y1 (= Y3 ). Consequently, if we have only the product ΔG 2, the equations ΔG 2 = ΔY 2 = ΔY1 should hold. | ||
| In conclusion, the Keynesian multiplier effect theory Is mathematically wrong. | ||