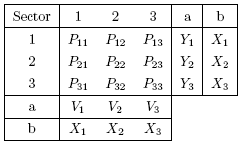
Chap2 Presentation of a New Cash Flow Matrix Analysis in Place of Leontief's Input-Output Analysis
Outline
Hayashi, Yuichiro Ph.D. (Eng.)
Dec., 2003(Publication) Apr., 2010(Revision)
This theory (the CF matrix analysis) points out errors in W.W.Leontief's input output analysis or the IO analysis ; the CF matrix analysis has been better developed referring to the IO analysis. The result from this analysis indicates the following: (1) Leontief's IO theory is wrong as long as only his basic equation in production is used; (2) his price model analysis is completely wrong; (3) multiplier effect due to Leontief's inverse matrix calculation for incremental final goods is never included in the IO analysis; (4) Eq.(15) which is a single basic equation in the CF matrix analysis will become one of the most important equations for financial analyses in the future.
Leontief's input-output table is shown in Table 1 in the case of three industrial sectors.
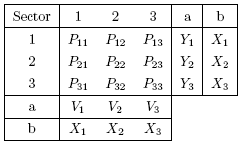
Fig. 1 Leontief's input output table
In Fig.1, the following notations are defined:
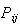 =intermediate
goods input or intermediate sales to other sectors ( cash
in-flow from j to i sectors);
=intermediate
goods input or intermediate sales to other sectors ( cash
in-flow from j to i sectors);
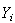 =final
goods (cash in-flow from final customers);
=final
goods (cash in-flow from final customers);
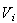 =gross-value
added provided to i sector ;
=gross-value
added provided to i sector ;
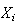 =i
sector's total sales which include those of intermediate and final goods. Note that import goods are the value-added provided by
foreign countries and export goods are the final sales to foreign countries. All
the symbols are expressed with monetary amount.
=i
sector's total sales which include those of intermediate and final goods. Note that import goods are the value-added provided by
foreign countries and export goods are the final sales to foreign countries. All
the symbols are expressed with monetary amount.
We assume that imports = exports = 0; the analysis of the case where imports and exports are not 0 will be made later in a formal research paper by the author. One does not need assumptions other than the condition that numerical values or symbols used in this analysis should fulfill an account system. Since no economic theories which do not satisfy accounts exist, in fact no assumptions are needed.
By means of the well known analytical method of Leontief's input output table, we have:
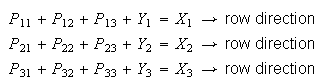
|
(1) |
Let define
 ,
where
,
where
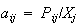 ,
as shown in Eq.(2), we obtain Eq.(3):
,
as shown in Eq.(2), we obtain Eq.(3):
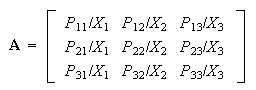
|
(2) |
Note that
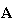 is not a symmetric matrix.
is not a symmetric matrix.
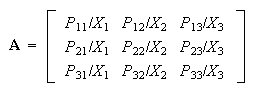
|
(3) |
Note that if Eq.(1) derived from accounts in accounting, Eq.(3) always holds
identically irrespective of whether variables such as
P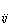 ,
Y
,
Y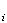 ,
V
,
V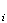 and
X
and
X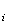 are linear, nonlinear, endogenous or exogenous, or of whether decision-making
behaviors exist.
are linear, nonlinear, endogenous or exogenous, or of whether decision-making
behaviors exist.
Eq.(3) is transformed into matrix form Eq.(4); further we have Eq.(5) and Eq.(6):
| (4) |
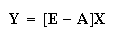
|
(5) |
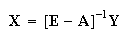
|
(6) |
where
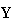 =final
goods
vector=
=final
goods
vector=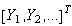 ;
;
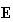 =unit
matrix (identity matrix), X=total output vector. Let the
intermediate product matrix be denoted P matrix.
=unit
matrix (identity matrix), X=total output vector. Let the
intermediate product matrix be denoted P matrix.
[The beginning of the author's new derivation]
With vertical operations, we obtain:
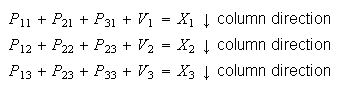
|
(7) |
When
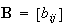 ,
where
,
where
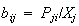 ,
is defined as shown in Eq.(8), Eq.(7) is transformed into Eq.(9):
,
is defined as shown in Eq.(8), Eq.(7) is transformed into Eq.(9):
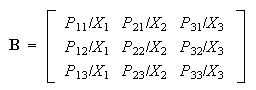
|
(8) |
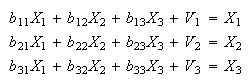
|
(9) |
When we define the gross value-added vector as
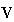 =
=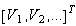 ,
we obtain Eq.(10):
,
we obtain Eq.(10):
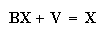
|
(10) |
From Eq.(10), we have Eq.(11) and Eq.(12):
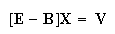
|
(11) |
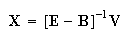
|
(12) |
From Eq.(6) and Eq.(12), we obtain:
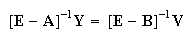
|
(13) |
When matrix
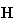 is defined as Eq.(14), we have matrices expression which directly connects the
gross value-added vector
is defined as Eq.(14), we have matrices expression which directly connects the
gross value-added vector
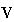 to the final product vector
to the final product vector
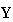 as Eq.(15) and Eq.(16):
as Eq.(15) and Eq.(16):
| (14) |
|
|
(15) |
|
|
(16) |
At first glance at Eq.(2) and Eq.(8), it appears
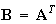 .
However, in fact
.
However, in fact
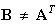 .
Confirm that Eq.(15) does not relate to Leontief's price model analysis.
.
Confirm that Eq.(15) does not relate to Leontief's price model analysis.
[The end of the new derivation]
Since
the
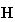 matrix will be used in a cash flow analysis in both business transactions and
economic analyses, including transfers and credit transactions, we shall
tentatively name the matrix the cash flow matrix or the
CF matrix.
matrix will be used in a cash flow analysis in both business transactions and
economic analyses, including transfers and credit transactions, we shall
tentatively name the matrix the cash flow matrix or the
CF matrix.
Although details are not explained here, the
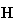 matrix merely expresses a form of intermediate transaction. Any changing
elements of
matrix merely expresses a form of intermediate transaction. Any changing
elements of
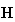 cannot alter the result of matrix operation. Since Eq.(15) is an identical
equation, the equation holds between
cannot alter the result of matrix operation. Since Eq.(15) is an identical
equation, the equation holds between
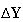 and
and
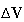 .
Depending on Numerical calculation example 2, both
.
Depending on Numerical calculation example 2, both
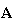 and
and
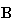 are independent of both
are independent of both
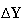 and
and
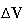 .
Consequently, we find that the concept of the "multiplier effect" or the
"ripple effect" by Leontief's inverse matrix operation is never included in
Leontief's input output analysis.
.
Consequently, we find that the concept of the "multiplier effect" or the
"ripple effect" by Leontief's inverse matrix operation is never included in
Leontief's input output analysis.
Numerical calculation example 1
Fig. 2 shows the example in which sector 1 's gross value added is given -50.
This situation might not occur in real economies but we face such a situation
in a financial crisis, a catastrophic disaster or a war. We can look at
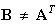 in
this example.
in
this example.
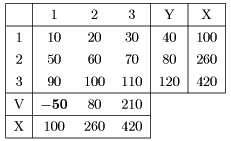
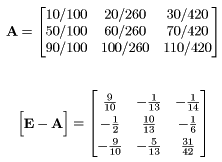
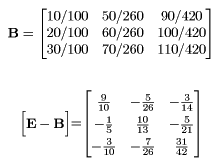
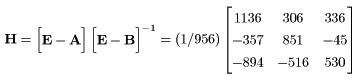
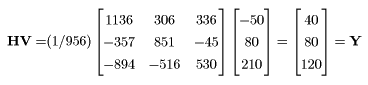
Fig. 2 IO table which has a minus value gross value added
Numerical calculation example 2
This example shows that the matrix
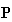 =
=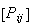 (
i, j=1,2,...) is independent of both vector
(
i, j=1,2,...) is independent of both vector
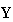 and vector
and vector
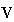 ;
we have an infinite number of solutions to
;
we have an infinite number of solutions to
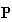 which satisfies the relation between
which satisfies the relation between
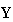 and
and
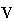 ;
thus, the solution of
;
thus, the solution of
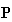 is indefinite. Fig. 3 shows the IO table of Japan, in a year, made up of 4
sectors, which has been reaggregated from the 13 sector table by the author.
is indefinite. Fig. 3 shows the IO table of Japan, in a year, made up of 4
sectors, which has been reaggregated from the 13 sector table by the author.
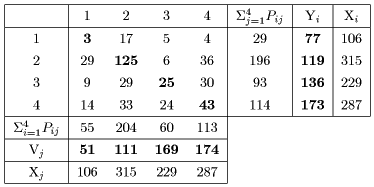
Fig. 3 IO table of Japan in a year
Fig. 4 shows that we can easily obtain
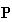 with arbitrary element values fixing
with arbitrary element values fixing
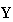 and
and
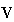 as constants.
as constants.
That is to say, the elements of
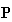 in Fig. 3 have been put those of a real business transaction form of
in Fig. 3 have been put those of a real business transaction form of
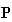 in any form of
in any form of
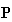 preserving GVA= GDP. Although it appears that many economical values exist in
Fig. 3, the whole value in X is only
preserving GVA= GDP. Although it appears that many economical values exist in
Fig. 3, the whole value in X is only
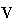 (=
(=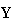 ).
The reason is as follows: in any enterprise's account, other enterprises'
previous sales amount is included in both sides of the account; the sum of the
intermediate sales amount
).
The reason is as follows: in any enterprise's account, other enterprises'
previous sales amount is included in both sides of the account; the sum of the
intermediate sales amount
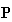 and the sales of the final product
and the sales of the final product
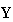 to the final buyers is
to the final buyers is
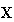 .
The relationship between
.
The relationship between
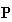 ,
,
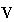 ,
,
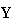 ,
,
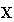 and H is
a regular Affine transformation which maps the vector V
to the vector Y when the matrix H is invertible. There is no
problem whether any element in the matrices and vectors is a plus or minus
value as long as their original account system is realistic.
and H is
a regular Affine transformation which maps the vector V
to the vector Y when the matrix H is invertible. There is no
problem whether any element in the matrices and vectors is a plus or minus
value as long as their original account system is realistic.
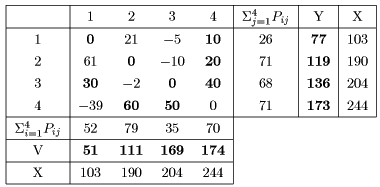
Fig. 4 Arbitrary elements in
In the
open Leontief system, since
 and
and
 are put outside of the matrix
are put outside of the matrix
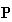 ,
we must give
,
we must give
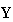 and
and
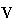 the whole value of the GVA respectively. The whole value
the whole value of the GVA respectively. The whole value
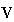 (=
(=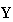 )
never increases nor decreases in Fig. 3. Consequently, since no values are
included in
)
never increases nor decreases in Fig. 3. Consequently, since no values are
included in
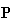 ,
,
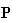 merely shows a form of business transactions in production.
merely shows a form of business transactions in production.
In the closed
Leontief system, the situation is the same as the open system as well. As long
as the production factors GVA( wages etc.) exists in the inside of the matrix
independently of goods
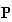 ,
,
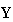 removed into the inside has the whole value GDP(=GVA), so that
removed into the inside has the whole value GDP(=GVA), so that
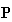 has no production values. In the
two cases, although we can give
has no production values. In the
two cases, although we can give 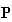 intermediate exchange values, we must understand that
intermediate exchange values, we must understand that ![]() and
and 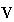 (=
(=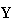 )
are independent of each other and
)
are independent of each other and 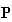 is a solution taken out of indeterminate solutions.
is a solution taken out of indeterminate solutions.
As another model, we can give every goods in
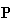 and
and
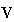 a part of the gross value added
a part of the gross value added
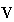 through each production. However, we cannot extract any value from
through each production. However, we cannot extract any value from
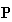 depending on the definition; Leontief did not adopt this type model.
depending on the definition; Leontief did not adopt this type model.
In short, the input-output table is an analytical model
to research a production process. If we concentrate production values
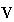 in final products
in final products
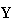 ,
the production values are not included in
,
the production values are not included in
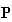 .
If we concentrate production values
.
If we concentrate production values
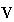 in
in 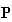 ,
the production values are not included in
,
the production values are not included in
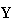 .
In fact a partial gross value added is given through each production process in small portions.
Their aggregated production value is
.
In fact a partial gross value added is given through each production process in small portions.
Their aggregated production value is 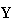 (=
(=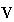 ).
).
Numerical calculation example 3
Fig. 5 shows a 2-dimentioal model and Fig.1 represents the Affine transformations for the vectors.
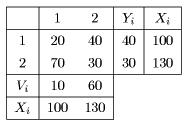
Fig. 5 2-dimensional model
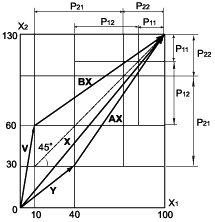
Fig.6 Affine transformations for vectors
An error in Leontief's price model analysis
Transforming Fig.1 into price p ×quantity q expression gives:
|
|
|
Fig.7 Transformation into price ×quantity expression |
where wqVj=Vj; for example, if we suppose that Vj is the total wages (a value- added) in the industrial sector i, qVj is a quantity of labors and w is a wage per unit labor i.e. a labor price.
Leontief's price model equation is obtained by the vertical operation in Fig.7. Dividing vertical columns by qi gives Fig.8. We can interpret that in Fig.8 each industry's total output quantity = 1 and qij/qj is an extended quantity.
|
|
|
Fig.8 Quantity transformation as qi=1 |
Vertical operation in Fig.8 gives the following:
|
(q11/q1)p1+(q21/q1)p2+(q31/q1)p3+wα1=p1 (q12/q2)p1+(q22/q2)p2+(q32/q2)p3+wα2=p2 (q13/q3)p1+(q23/q3)p2+(q33/q3)p3+wα3=p3 |
(17) |
where αi=qVi/qi.
Defining the notation as Eq.(18) gives Eq.(19).
|
bij=qji/qi |
(18) |
|
b11p1+b12p2+b13p3+wα1=p1 b21p1+b22p2+b23p3+wα2=p2 b31p1+b32p2+p33p3+wα3=p3 |
(19) |
Using the notation B defined in Eq.(8) and Eq.(9) gives
the following:
|
Bp+wα=p |
(20) |
where price vector p=[p1,p2,p3]T, α=[α1,α2,α3]T. From Eq.(20) we have:
|
p=w[E - B]-1α |
(21) |
Leontief used A matrix toward the column direction in Eq.(4) in the transformation process from Eq.(17) to Eq.(22) . This operation is clearly wrong because B≠AT.
|
ATp+wα=p |
(22) |
We cannot interpret that Eq.(21) is the correct solution of the price model analysis on the basis of obtaining Eq.(20). The reason is that the solution of the IO table equations shown in Fig.1 is the only one Eq. (15). If we regard Eq.(21) alone as the correct solution, we will have a wrong solution with a multiplier effect.
The fundamental cause of Leontief's IO analysis' error results from the derivation method of equations itself. The IO table expresses, e.g. in the 1st industry, the account: debit=P11+P21+P31+V1, credit=P11+P12+P13+Y1 and the total of debit=the total of credit=X. Although the numerical value of each symbol in the table is asymmetric, the array of the symbols is symmetric. In the process of deriving equations, the symmetric property of symbols in the row and column directions must be kept like the operations for Eq.(3) and Eq.(9). As a result, the same shaped equations as Eq.(4) and Eq.(10) are derived; the notations of A and B in Eq.(2) and Eq.(8) must be used because of the asymmetric property of the numerical value of each symbol. In Leontief's IO analysis the symmetric property in the process of deriving equations in the row and column directions is not kept. Consequently, even if the correct Eq.(20) is used in place of Eq.(22) , the error of the IO analysis method cannot be eliminated.
As analyzed above, the relationship between prices and quantities for produced goods is given as obvious solutions: one side solutions are the total of Vi(= price× quantity) = the total of Yi (= price×quantity); other side solutions of price and quantity for Pij are indeterminate ones because we have an infinite number of Pij (= price×quantity, intermediate outputs) which satisfies Fig.2.
In conclusion, although the IO table is very useful, all the existing analytical results used Leontief's input output analysis for economies are wrong. The reason is that the correct solution for the open type production equation including the price model equation is given by the only one Eq. (15). However, Leontief's achievement of the input output analysis theory has never been detracted by his mistake because he presented the original methodology the IO table analysis for economic analyses.
In addition, when an investment fund F is supplied to a single industrial sector, the multiplier effect of F in production to other industrial sectors of course exists as far as the effect does not reach the fund provided. That is to say, F(=GVA) is distributed to other industrial sectors. The author's claim shown in the term (25) in §6 is that even in this case, the part 'F×marginal propensity to consume' must be supplied to consumption goods i.e. 'investment fund F is provided to consumption industries too'. (June/29/2010).
Detailed paper will be published in a few days.
Notice! Discriminate between P matrix, p vector, A matrix and B matrix.
This description was first published on Dec. 12, 2003 and rewritten on Dec. 3, 2009; Correction of notations on July, 2010.
§1 Development to Business Input-Output Table (Japanese)
§2 Presentayion of the Cash Flow Matrix (CF Matrix) Analysis for National Accounts and a Consideration of the Leontief Input Output Analysis Theory