§5 Additional Examination

DCE  Yuichiro Hayashi
An increase or cut in taxes doesn't show the multiplier effect.
For analyzing the unemployment problem, the break-even type chart should be used.

July 1, 2004
5.1 Economic effect of an increase or cut in taxes
The conventional theory is as follows:
                            C 2 = a A +  a K ( Y 1 -T1 ),     T1  :   Taxes                     (5-1)
                            Y2D = C2 + I 2 + NX 2 + G2                                              (5-2)
Substituting Eq.(5-1) into Eq.(5-2) gives, at the Keynesian cross,:
                            Y =a A +  a K ( Y 1 -T1 )+ I 2 + NX 2 + G2                       (5-3)
If we assume that a A , I 2, NX 2 and G2 are constant when Y→Y + ΔY and T1→ T1+ΔT1 in Eq.(5-3), we have: 
                       ΔY/ ΔT1 = - a K / (1 - a K)                                                    (5-4)
Eq. (5-4) is wrong( incorrect/ flawed). We can't adopt the above-mentioned assumption. Furthermore, we should know that T1 is a transfer in income. The transfer in income returns to the income through production, or it moves from some people to other people. These are redistributions of income.
We should strictly consider the domain and the range of this problem. One fiscal time period should be set up. In this period, all economic data which include incremental taxes should be consistent with one another.
In this analysis, it is assumed that both net factor income and net transfers, from abroad are zero. The analysis is possible between NDP and NDI without the assumption, but we can't use the term "disposable income". A national government finance is shown in Table 5-1. This table shows market price. 

Table 5-1 National government finance

Taking national government finance into consideration, we have a table showing NNI and the corresponding production, (if we take off debts and credits relationships other than government terms), in Table 5-2. In this table, the notations on production are shown at factor cost.

Table 5-2 NNI at factor cost

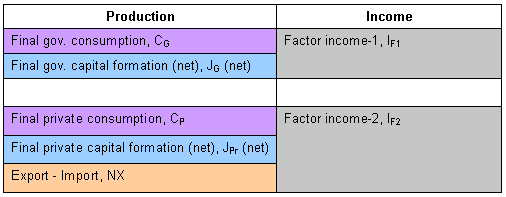
Net value added is equivalent between production and income. Therefore, disposable income is divided into the government sector and the private sector as shown in Table 5-3.

Table 5-3 Dividing of disposable income

where 
                                IF = IF1 + IF2                                                                   (5-5)
When we express Table 5-2+ with cash flow, Table 5-2 changes into Table 5-4:

Table 5-4 Cash flow 

If we take away the distribution role of government, Table 5-4 is transformed into Table 5-5:

Table 5-5 Transformation from Table 5-5

In Table 5-5, the word "enforcement" refers to enforcement by the government. The word "Certificate" means that it is a bond certificate on which the government has promised the paying of debts for private people, directly or via banks. 
From Table 5-4, we obtain:
        TxID + CG +  CP + JG(net)  + JPr (net) + NX 
        = TxID + (TxD - TxD) + IF  + (Ts1 - Ts1) + (Ts2 - Ts2) + (BG - BG) + Certificate          
                                                                                                                            (5-6)
Eq.(5-6) is equivalent to : 
        CG +  CP + JG (net)  + JPr (net) + NX  = IF + Certificate                       (5-7)
 Eq.(21) and Eq.(22) are linear equations, therefore these equations hold between incremental terms. In Eq.(21), we can't find the tax multiplier effect - ( MPC / (1-MPC) ) ·Tax.  
The true relationship between tax and consumption will be investigated.  First of all, incremental indirect taxes are included in both sides of Eq.(5-6) in the same amount, therefore they don't mathematically affect production. 
If we increase incremental direct taxes, some people have to pay the taxes, and they therefore may decrease private consumption. However, in this case, the government consumption or the net government investment will increase by the incremental amount of  tax. 
This relationship holds for the incremental security transfers. If the incremental  security transfer Ts2 increases, those people paying may decrease their consumption, but the beneficiaries will surely increase incremental consumption. Purchase of bonds, by original definition,  doesn't relate to consumption. Consequently, incremental taxes don't mathematically effect total consumption. This phenomenon occurs because both taxes and security transfers are transfers between some people and other people in income.
However, this is a mathematical discussion. It should be noted that the relationship between all terms in Table 11, holds  among all contracts, and it is executed little by little throughout a year. In this process, the psychological effect of taxation may effect private consumption. 
 
This will be explained a little more deeply. An economic transfer between, for example, households and a government doesn't affect the total (or the average) of disposable income. However, it should be noted that economic activities by people result from the accumulation of each small contract (or unit of work). The contract is really the accumulation of unit activity, by a person and a machine, whose value is measured by the gross value added.  Each contract( or activity) is generated suddenly , and it  increases or grows little by little. On the other hand, a contract  which has finished its economic role, dies little by little. The economy is made up of vital activities. Each economic transfer is, as a matter of course,  one of the vital activities, and yet it does not( or hardly)  use economic active energy( GVA).
In summation, economic transfers are like catalysis in the economy, that is to say, enzyme action in biochemical responses. The catalysis creates an atmosphere in the economy , and it accelerates or decelerates economic responses. Catalysts take effect both for acceleration and suppression of biochemical responses. 
  
Economic transfers are tools for social redistribution of incomes. If economic transfers are effective for the economy, it will be in a favorable business condition, and vice versa.  To describe this phenomenon, I used  the word "psychological effect", though it would also be appropriate to use the terms " atmosphere effect" or " catalysis effect".
By the way, the debtor-creditor relationship resembles the transfer relationship in that both of them are processed between cash and cash in accounts. The former is accompanied by repayment obligation certificates, but the latter is executed without conditions. The debtor-creditor account processing may be interpreted that it is twice transfer procedures, and what connects the two procedures (time period) is credit (honor) .
In Table 11, the certificates are, in fact, exchanged between some people and other people, both of whom now live but will not live in the future. However, in Table 10, the certificates are exchanged  between some people and the government. Consequently, an outstanding government bonds problem must be resolved within generations where bonds  have been issued, including retired generations. 
 
Incidentally, just as economic transfers are tools of redistribution in income aspect, the transfers are also tools of redistribution in production. Therefore, the government bond problem is the income redistribution problem, but at the same time, it is an industry redistribution problem also. 
There is a possibility that the above-mentioned logic is different between free economy and controlled economy, because in the latter economy, induction of purchase by free will might virtually change into enforcement by a rationing system.
5.2 Two kinds of economic charts in the national accounts or in business accounts
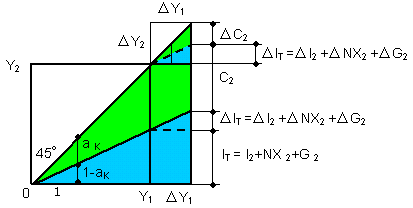
The equations previously defined are rewritten here:

Y2 = C2 + I 2 + NX 2 + G 2

(5-L1)

Y1 = TxID+  W+ P + D

 (5-L2)
where TxID = Taxes less subsidies, W = employees compensation, P = operating surplus and D = capital depreciation

Y2 = Y1

 (5-L3)

ΔY2 =Δ C 2 + ΔI 2 + ΔNX 2 + ΔG 2

(5-L4)

ΔY2 =Δ Y1

 (5-L5)
We have two types of economic goods charts. One is a time-series type( or proportion type) chart, and the other is a break-even type input-output chart.  
 
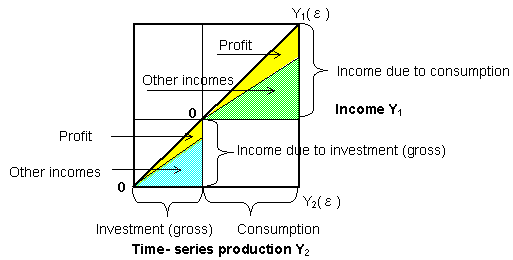
A time-series type chart in a national account of a fiscal year is expressed as shown in Fig.5-1.  

 
                                   Fig.5-1 Time-series type chart
In the time-series type chart, even capital depreciation( death of partial, old capital formations) will, in fact, change with yearly time processes, and at the same time, new capital formation (gross), i.e. investment goods will be generated according to the capital depreciation with new net capital formation. 
The horizontal axis shows realized, cumulative production output. The vertical axis shows components of realized, cumulative income( input). The time-series amount can be monthly cumulative one, or yearly final one for long years.
The characteristics of this chart are as follows: 
(1) The band width of operating surplus( 'profit' in Fig.5-1) shows a part proportion of the wholeY1. This holds in other components.
(2) As the operating surplus is a function of one variable Y2, Y2  is uniquely determined for a given operating surplus, if the economy is in a stationary condition.
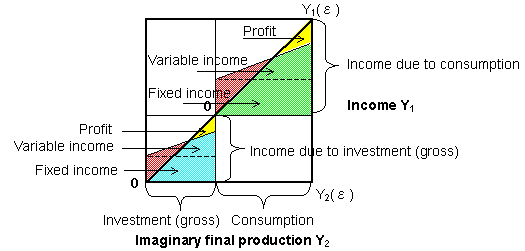
A break-even type chart is shown in Fig. 5-2. 

                                  Fig.5-2 Break-even type chart 
On the other hand, in the break-even type input-output chart of a firm, capital depreciation and other fixed costs are treated as constants within a year.  When we liken a national economic account to an income statement of a firm, we can make break-even charts for main products, for example, C2 and IT( investment). In this kind of chart, the realized amount point is for only the end point which is placed above the final product on the horizontal axis. The characteristics of this chart are as follows: 
 
(1) Any point on the intermediate position of the 45 degree line connecting the origin to the end point shows an imaginary coordinate point( imaginary output, imaginary input).
(2) The operating surplus( 'Profit' in Fig.5-2) is a function of three variables, a fixed income,  a variable cost ratio and a final product Y2. If we take stocks into consideration in this type of chart, we can draw the 'break-even line' as described in §1 in "Management Accounting".
In both charts, the total input-output points move on the 45 degree line. As each yearly Y2 is similar in expression in the two charts, the concepts of these two charts are prone to be misunderstood.
 
The Keynesian's consumption function is made out of the concept in Fig.5-1. What kind of information can we expect  for the additional government expenditure ΔG  from this chart? The answer will be that the yearly average proportion of ΔG( revised additional amount)  to G (amount on initial budget) can be calculated. The income change corresponding to ΔG is, as a matter of course, the same amount as ΔG. However, the total income doesn't change, because ΔG is a transfer between some people( or firms) and other people( or firms).
 
On the other hand, the input- output table chart in the national economic accounts is made out of the concept in Fig.2. Business entrepreneurs always act in such a manner that they try and get as much profit as possible depending on the various, present economic atmospheres (catalysis). Each business entrepreneur judges his firm's dismissal problem with its break-even chart, because in this chart, the relationship between costs including wages and profit( or loss) is expressed. 
 
Furthermore, he knows that the time-series type chart can't give any information to resolve management problems in a unsteady economic motion. For example, he doesn't get the information of loss information from the time-series type chart. In addition, he instinctively knows that a profit is a function of three variables, fixed costs, efficiency( variable cost ratio) and sales amount. 
 
Even If we know a profit in statistical data, we can't know the background of the profit from the time-series type chart, that is to say we don't know moving of other two variables than a total sales. On the other hand, in a stationary economic flow, the time-series type chart will effectively utilized because it is a simple chart to understand. 
 
A national unemployment problem is same as a dismissal problem in firms. For analyzing the unemployment problem in a unsteady economic circumstance, the break-even type chart should be used.
 
5.3 Behavior of a two-degrees of freedom system
The input -output system, with two-degrees of freedom in an economy, is a simple mathematical problem.
Consider the following equation:
                       z = x + y                                                (5-1)  
Suppose that the whole z is composed of its components both x and y, which then makes a (z,  x, y)-system with a two-degrees of freedom. Let z be a function of time because this is an economic problem. We consider the following cases:
case(A)  Both x and y are mutually independent variables with respect to time;
case(B)  Only x is a variable with respect to time, and y is also a variable but is not so with respect to time.
When we add the following one constraint condition Eq.(5-2) to the (z,  x,  y)-system, we can investigate what occurs:
                    x = kz + b                                                 (5-2)  
where k and b are constants with respect to time.
From Eq.(5-1) and  Eq.(5-2), we have:
                     Δz  =Δx + Δy                                          (5-3)
                     Δx = kΔz                                                 (5-4)  
From Eq.(5-3) and  Eq.(5-4), we have:                    
                     Δy = (1 - k)Δz                                         (5-5)
                     
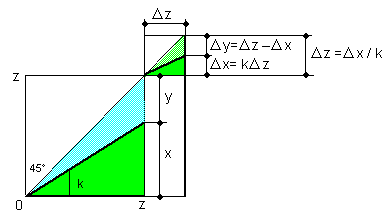
In case (A), the (z, x, y)-system becomes a one-degree of freedom system when the constraint condition Eq.(5-2) is added to the system. In this system, the representative variable is Δx, when all the amounts, Δz, Δx /k, Δx + Δy and Δy /(1 - k) are the same. This is shown in Fig.5-3 (below) . Note that Δx can change with respect to time.

Fig.5-3
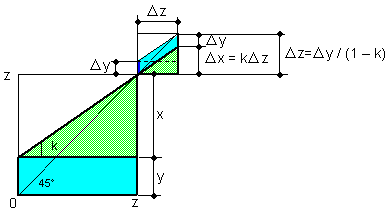
In case (B), the equations with respect to time can be solved as follows:
                  Δz = Δy / (1 - k)                                      (5-6)
                  Δx = Δy ∙ k / (1 - k)                                 (5-7)
where Δy is a variable which is independent of a change in time. The word 'solved' means that variables with respect to time are already determined or time stopped. Only Δy can change, which is a function of a factor other than time, for example, the accidental nature of peoples' will. Δy must always be determined in the beginning of the change Δz. The whole Δz must be linked to only Δy. Note that Δx in Eq.(5-7) should automatically be generated at the same time as Δy is generated, because Δx can't change any longer with time. 
 
This is shown in Fig.5- (below).
Fig.5-4
 
case(C) Both x and y are mutually independent variables with respect to time. x is divided into two parts, as in x = x1+ x2. At the same time,  Eq.(5-2) holds; 
We denote x as:
                   x = x1 + x2                                             (5-8)
Eq.(5-1) and Eq. (5-8) give:
                    z = x1 + x2  + y                                     (5-9)
Eq.(5-9) with Eq.(5-2) seems to be a 2-degrees of freedom system. However, both x1 and x2 are one pair of (x1, x2) which satisfies Eq.(5-8). Thus, the system with both  Eq.(5-9) and Eq.(5-2) is one-degree of freedom system.
case(D) Only x is a variable with respect to time. y is also a variable but is not so with respect to time; y is divided into two parts as y= y1+y2; At the same time,  Eq. (5-2) holds. 
We denote Y as follows:
                    y = y1 + y2                                           (5-10)
As shown in Eq. (5-9), we have: 
                  z = x  + y1 + y2                                      (5-11)
As both y1 and y2 are halves of the pair (y1, y2), which satisfies Eq.(5-10), this system is also a one-degree of freedom system.
 
The important point of the two cases, (case(C) and case(D)), is that, for example, both the variables y1 and y2 are halves of (y1, y2). Consequently, when we select y1 as a variable in this system, we have to remember the existence of y2, and have to provide y2 in the system.  
   
5. 4 A reconsideration of the ΔY1 = ΔI2  / (1 - MPC) chart problem  
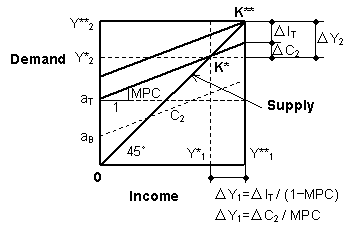
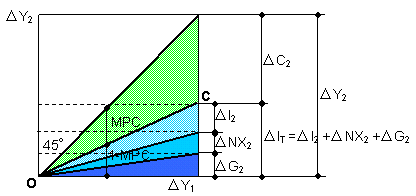
Using the assumption ΔG2 = ΔNX2 = 0 in Fig.3-2, we can obtain Fig.5-5 where  ΔI2 is expressed as ΔIT. We can also get the same chart when we assume that ΔG2 and ΔNX2 are included in ΔIT. This chart is used in the economic model which J. M. Keynes adopted in his original work, although he didn't show its model chart. We shall call this chart  'Keynes' original chart'.

 

 Fig.5-5 Keynes' original chart
 
In Keynes' original chart, the Keynesian cross condition is satisfied. Is there any strange point in this chart in the time series real economy when the MPC exists? 
 
When we analyze an unemployment problem using Keynes' original chart, several important shortcomings occur.
 
We will examine the validity of Keynes' original chart using the argument shown in 5.3. We apply the following notations: z = Y2,  x = C2, y = IT and k = MPC. Keynes' original chart corresponds to the case(B) or the case(D) in 5.3. 
 
(S1) According to the case(B), ΔY2 is a function of only ΔIT which doesn't relate to a change in time. This property reaches IT and Y2, because assuming that this property is applicable to only both ΔIT and ΔY2 is illogical. Hence, the characteristics of the economy which Keynes' original chart implies, will be as follows: 
 
In Keynes' original chart theory, the whole ΔY2 , i.e. both ΔC2 and ΔIT doesn't change with time but rather by the uncontrollable fluctuations of people's decisions. Furthermore, ΔIT must always be provided before the finished change ΔY2. In short, the economy expressed by Keynes' original chart is one where both IT  and C2 don't relate to the passage of time. This society is one where ergodecity is assumed. This might be similar to a preindustrial society.
Let's imagine this economic model in a little more detail. The investment goods ΔIT are composed of many goods as in ΔIT = ∑iΔITi.  A good ΔITi is provided at any  time, so ΔITi doesn't have a functional relationship with time. As soon as ΔITi is produced, ΔC2i = ΔITi ∙ MPC / (1 - MPC) is also produced. In short, a pair of goods ΔITi +ΔC2i = ΔITi / (1 - MPC) is instantly produced.  
 
In this economy, consumption is not allowed to move freely but should completely depend on changes in investments. Such an economy might occur in a fully communist society. This is the first shortcoming. （24.Feb.2005)   
This economic model might be appropriate in analyzing a distribution problem of economic goods or incomes, but it is not suitable  for analyzing a dynamic economic problem of an unsteady economic situation in a capitalist society. This viewpoint is important in particular when analyzing the national, large-scale problems of the capitalist country in an unsteady state of economy, i.e. a significant unemployment problem;
(S2)The next large shortcoming in Keynes' original chart theory occurs just when ΔG2 is supplied in order to resolve an unemployment problem. This will be explained using  Fig.5-6. Let ΔIT be ΔIT = ΔI2 + ΔNX2 + ΔG2. When we select ΔG2 as a variable corresponding to one degree of freedom in an economic analysis, we have to consider the roles of remaining ΔI2 and ΔNX2 at the same time, and have to take them into consideration in the analysis.

Fig.5-6
By virtue of Keynes' original chart theory, the equation  ΔY1= (ΔI2+ ΔNX2 + ΔG2) / (1 - MPC) can be derived. The MPC is defined for ΔIT. Consequently, both ΔI2 and ΔNX2, as well as ΔC2, have to be simultaneously and instantly provided with the production ΔG2. This brings up a puzzling situation. Now that we can't produce ΔI2 and ΔNX2 instantly, according to the supply ΔG2, the multiplier effect theory has been used for analyzing an unemployment problem; (4.Mar.05)
In the real economy, it is observed that the economy doesn't necessarily depend on only the investments which brings instant consumptions. This was confirmed by the Japanese economic phenomenon in which GDP did not increase despite an increase of government investment during a business depression. Consequently, the real economy doesn't move in a manner that Keynes' original chart shows.  Keynes' original chart theory doesn't help to resolve an unemployment problem.
The case(A) in 5.3 is a more likely economy. However, we can't control consumption connecting to the whole GDP(=C/k), in a capitalist society.  And J.M.Keynes didn't insist upon this logic.
In the real economy, both C2(t) and IT(t) are mutually independent variables of time, apart from NX2(t) and G2(t) .  This denies the existence of the MPC.
 
However, the MPC is factually found by statistical observations of the real economy as shown in Fig. 3-11. In this chart, the shapes of the two triangles of C2 and IT are really nonlinear shapes. How can the MPC be observed in the real economy?

 Fig. 3-11
 
Remember that the profit of a company is determined by the three degrees of freedom;  a fixed income,  a variable cost ratio and final sales Y2. These three factors are closely connected with a dismissal problem. Suppose that a profit target for each company is determined both in C2 and IT industries in advance. Entrepreneurs manage their firms trying to reach each profit target with the result of either expansion or contraction of firms. This might generate more hiring or more dismissing.
 
Production in a national economy is an aggregation of all firms' activities.  In the national economy, costs and profits in firms are equal to the source money of buyers' purchasing power. Buyers select to purchase either consumption goods or investment goods, deciding to either consume or save. Within the category of 'buyers', unemployed people are included. In addition, the proportion of consumption( expenditure to short life goods) to investment (saving of long life goods) in each country is the unique individual shape of its own economy. 
 
Therefore, I think that the MPC can be obtained only when we look at the resultant moving of consumption in a many degrees of freedom economic system in a stationary economy. By endeavoring to keep each firm profitable and by the national propensity to consume, the MPC would have been kept constant in the stationary economy. However, in an unsteady economy, both ΔC2 and ΔIT( or Δ gross saving) will probably move freely. Behind an amount of the MPC, the influence of entrepreneurs' efforts for profits, unemployed people, expansion or contraction of firms, fortune and misfortune etc. are concealed. When they exceed certain limits,  the MPC will move turbulently.
 Last updated: 5/Mar/2005