Derivation of the managed gross profit chart and the 45 degree break-even chart under absorption costing

Part 1 Management Accounting

§1 Derivation of the managed gross profit chart and the 45 degree break-even chart under absorption costing

Yuichiro Hayashi, Y. Hayashi

The CVP analysis or the break-even analysis is easily possible in business accounting under standard costing or absorption costing.

This section describes the main points of the references (1) and (2).

The reference (1), an invention applied for in 1997 as a business patent to the JPO is termed the "1st invention". The reference (2), the U.S. patent is termed the "2nd invention".

Cost accounting is classified into main branches of both absorption costing or full costing (a representative example: standard costing) and direct costing or variable costing. The big difference between the two costings is the treatment of manufacturing overheads (fixed indirect cost) for product costs. In absorption costing, the manufacturing overheads are distributed to goods sold and inventories by allocation. In direct costing, it is treated as a period cost in the same way as selling, general and administrative expenses (SGA), and so it is not distributed to inventories.

An income statement for financial accounting is ultimately made on the basis of absorption costing. The 1^st and the 2^nd inventions relate to charting the income statement under absorption costing. Both the 1^st invention and the 2^nd invention use the concept of the “managed-gross-profit” denoted by the symbol Q^M is used as a profit management target in management accounting. The symbol Q^M is defined as: Q^M = sales − manufacturing direct costs − manufacturing overhead applied. The Q^Mchart is termed the” managed gross profit chart”. In this chart the operating profit on an income statement (referred to as "the sales operating profit" ) is shown including the managed gross profit.

In the 1^st invention, a charting method for the managed-gross-profit chart for an overall company is described. In this invention, a break-even point which is shown in the managed gross profit chart is indicated, and the author has given a new, correct, break-even sales formula.

In the 2^nd invention, a break-even chart, under absorption costing, expressed as a 45-degree line chart is presented. In addition, a method of drawing the managed gross profit chart of each operating department in a company is presented.

For simplicity, we assume that manufacturing direct costs are actual costs. Manufacturing overhead is allocated to goods sold and inventories based on the predetermined allocation basis: manufacturing overhead applied = manufacturing overhead application rate × basis amount for allocating overhead. The symbol (ε) is added to any symbol X like X (ε) to show that X (ε) is a figure on a final income statement. Superscripts X and Y are used when cost items concern goods sold and goods manufactured, respectively.

The following notations are used per one company:

　X=sales

　D^X=manufacturing direct costs( actual and variable costs)

　C=manufacturing overhead ( actual and fixed costs)

G=selling, general and administrative expenses (SGA) ( actual and fixed costs)

A^X=manufacturing overhead applied to goods sold including beginning inventories

A^Y=manufacturing overhead applied to goods manufactured including ending inventories

　E^X=(D^X＋A^X) = manufacturing full cost of goods sold

Q^S=gross profit for goods sold or sales gross profit

π^S=operating profit for goods sold or sales operating profit

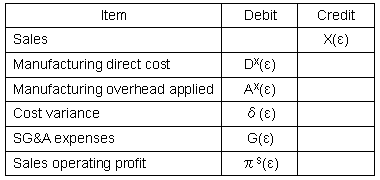
Manufacturing overhead applied included in goods sold is represented by the symbol A^X (ε). At the beginning of a fiscal year, the manufacturing overhead applied in a carried-down inventory is represented by the symbol A^X(−)(ε). At the end of the fiscal year, that in a carried-forward inventory is shown by the symbol A^Y(+)(ε). The manufacturing overhead applied, which is not included in inventories, is denoted as the symbol A^{X (0)} (ε) or A^{Y
(0)} (ε). The symbols D^X(−), D ^X(0) and D^{X (+)} are defined similarly. The relationships between these symbols are shown in Fig. 1-1.

Fig. 1- 1 Relationships between applied manufacturing overhead costs

The difference between A⁽⁻⁾(ε) and A⁽⁺⁾(ε)is defined by the symbol η (ε):
η (ε) = A^X⁽⁻⁾(ε) − A^{Y (+)}(ε)
= A^X (ε) − A^Y (ε)	(1-1)
The symbol η (ε) is called the "net carryover manufacturing overhead applied in inventories".

The manufacturing full cost E^Xof goods sold is defined as follows:
E^X= D^X＋A^X	(1-2)

Further, we define the "managed gross profit Q^M" as　follows:
Q^M=X − E^X	(1-3)
In the case where the symbol (ε) is not used in e.g. X, X refers to a value during the period.

In addition, the following notation is defined:
π^M (ε) = Q^M(ε)− G(ε)	(1-4)
,where π^M(ε) is called the "managed operating profit".

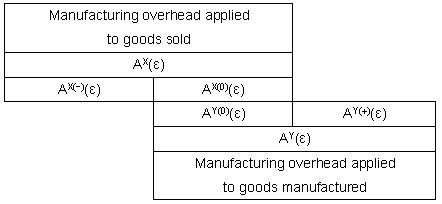
As the manufacturing overhead applied corresponding to the actual cost C (ε) is A^Y (ε), cost variance δ (ε) in a manufacturing overhead department is expressed as:
δ (ε) = C (ε) − A^Y (ε)
= C (ε) − (A^X (ε) − η (ε))	(1-5)
,where δ (ε) is positive when the manufacturing overhead applied is under-estimated comparing to C (ε) . When we directly charge δ (ε) to the current sales, the manufacturing overhead in goods sold is shown in Fig.1-2.



Fig.1-2 Manufacturing overhead in goods sold

An income statement for sales operating income in absorption costing is shown in Table 1-1.

Table 1-1 Income statement for sales operating profit

From Table 1-1, we have:
π^S(ε) =X (ε) − ( E (ε)＋δ (ε)) − G (ε)	(1-6)
In companies of order-initiated industry, manufacturing worksite persons regard E (ε) as a manufacturing cost control target; sales site persons regard Q^M (ε) as a profit management target. At the final stage of making an income statement, Q^M (ε) is transformed into the sales operating profit π^S(ε) using by G (ε) and δ (ε) as shown in Eq.(1-6) .

From Eq.(1-6), we obtain:
Q^S (ε)=Q^M (ε) − δ (ε)	(1-7)

Table 1-1 is equivalent to Table 1-2.


Table 1-2 Income statement-2


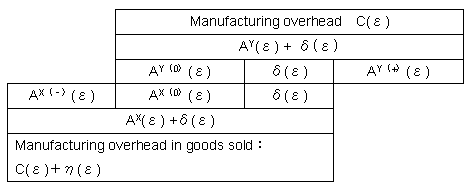
From Eq. (1-5) and Eq. (1-6), we have:
π^S(ε) = Q^M (ε)＋A^X (ε) − (η (ε)＋C (ε) +G (ε))	(1-8)
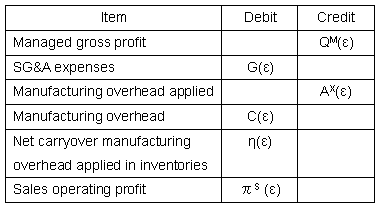
Eq.(1-8) shows that the following relationship shown in Table 1-3 exists.

Table 1-3 Income statement-3


The purpose of the managed gross profit chart theory is charting Eq. (1-8).　When we want to draw the break-even chart under absorption costing at the end of an accounting period, we must previously determine the line shapes of all costs from X=0 to X=X(ε) on the horizontal axis. Letting X be a variable of sales, both A^X(X) and A^Y (X) can be expressed with a combination of variable functions and constants. What shape is the function η(X) = A^X(X) − A^Y(X)? It is clear that the shape of η(X) is an important point in order to draw the break-even chart under absorption costing.

Both the 1st and the 2nd inventions resolved this problem. In conclusion, η(ε) becomes the constant which is determined by η(ε) = A^X(X) − A^Y(X)=A^X(−)(ε) −　A^Y(+)(ε). That is to say, we can regard η(ε) as a fixed cost. Details are given in the section, "The cause of Solomons's error in his break-even chart for absorption costing", §5, Part 1 on this website.

A ^X(ε) is determined based on an allocation basis. In charting Eq. (1-8), classifying the following two cases for A ^X(ε) is possible:

(1) A ^X(ε) is proportional or quasi-proportional for sales X (ε). The manufacturing overhead applied of this case is called the “1^st kind of manufacturing overhead applied”, and the notation of A ^XI (ε) is used.

(2) A ^X(ε) is constant or quasi-constant for X (ε). The manufacturing overhead applied of this case is called the "2^nd kind of manufacturing overhead applied”, and the notation of A ^XII (ε) is used.

Based upon this classification, the following notation is used:
A ^{XI, II} (ε) = A^X (ε)
= A^XI (ε) + A ^XII (ε)	(1-9)

If we also adopt the same classification for C (ε), we obtain, from Eq. (1-7), the following equation:
π^S(ε) =Q^M (ε)+A ^XI (ε) +A ^XII (ε) - (η ^{I, II} (ε) + C^{I, II} (ε) + G (ε))	(1-10)

As both C (ε) and G (ε) are fixed costs, Eq. (1-9) becomes:
π^S(ε) = Q^M (ε) +A^{X I} (ε) - f (ε)	(1-11)
f (ε) = f _C(ε) - A ^XII (ε)	(1-12)
f _C(ε) = η ^{I, II} (ε) + C^{I, II} (ε) + G (ε)	(1-13)

A marginal condition of Q^M (ε) in Eq. (1-10) occurs when π^S(ε) =0. Under this state, Q^M (ε) is represented with subscript ξ as in Q ^M_ξ(ε) . Thus Q ^M_ξ(ε) can be given by:
Q ^M_ξ(ε) = f (ε) - X (ε) · tan α(ε)	(1-14)
,where
tan α^XI (ε) = A ^XI (ε) / X (ε)	(1-15)
Transforming Eq. (1-14) gives
Q ^M _ξ(ε) / f (ε) + X (ε) / (f (ε) / tan α (ε))=1	(1-16)

Rectangular coordinates with the horizontal axis X and the vertical axis Q^M will be set. It is found that the point (Q ^M_ξ(ε), X (ε)) is placed on the following line at X= X (ε):
Q^M / f (ε) + X / (f (ε) / tan α(ε))=1	(1-17)

From Eq. (1-14) and Eq. (1-5) , we obtain
Q^M _ξ (ε) = G^F (ε) + δ (ε)	(1-18)
From Eq. (1-11), Eq. (1-5) and Eq. (1-18), we have:
π^S(ε) = Q^M (ε) − Q ^M_ξ (ε)	(1-19)

From Eq. (1-3) , we have:
Q^M (ε) = X (ε) − D^X (ε) − A ^XI (ε) − A ^XII (ε)	(1-20)
When X (ε) =0 in Eq. (1-20), the following equation is satisfied:
Q^M (X=0) = − A ^XII (ε)	(1-21)
Therefore, Q^M (ε) is written as:
Q^M (ε) = − A ^XII (ε) + tan β (ε) ·X (ε)	(1-22)
,where
tan β (ε) = ( A ^XII (ε) + Q^M (ε) ) / X (ε)	(1-23)

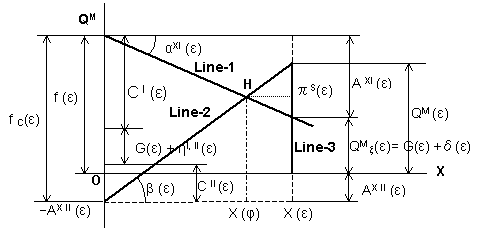
The managed gross profit chart consisting of the above-mentioned equations is shown in Fig. 1-3. Line-1 shows Eq. (1-16). The line is referred to as the “marginal managed gross profit line”. Line-2 shows Eq. (1-22). The line is referred to as the “managed gross profit ratio line”. Line-3 shows Eq. (1-6). Line-3 is referred to as the “managed gross profit line”. It should be noted that the slope of Line-2 is not equal to the ratio Q^M (ε) / X (ε) in the defined technical term when A^XII (ε) exists.

Fig. 1-3 Managed gross profit chart


In Fig.3, the intersection point H of Line-1 with Line-2 is the break-even point in absorption costing. If we denote the break-even sales by X (φ), X (φ) is given as the solution of Eq. (1-16) and Eq. (1-22) as follows:

X (φ) / X (ε)= ( η (ε) ^{I, II} + C^{I, II F} (ε) + G ^F (ε) ) / (X (ε) - D^X(ε))	(1-24)

Eq. (1-24) is different from Solomons’s formula known as the break-even sales in absorption costing. The author( Hayashi) carefully compared his theory and Solomons's theory with the ' Break- even line theory' which was the fundamental theory for this problem. He has verified that his theory is consistent with the break-even line theory but Solomons's theory is not. Therefore, Solomons's formula is wrong. Detailed descriptions can be found in Reference (2).

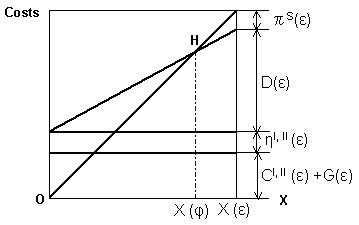
Fig. 1-4 shows a 45° break-even chart using the same accounting items as shown on Fig. 1-3. It is proved in Reference (2) that the break-even sales X (φ) on Fig. 1-3 and Fig. 1-4 are equal to each other. If η ^{I, II}(ε)=0 in Fig. 1-4, Eq. (1-24) reduces to the well-known breakeven sales formula in direct costing.

Fig.1-4 45° Break-even chart in absorption costing

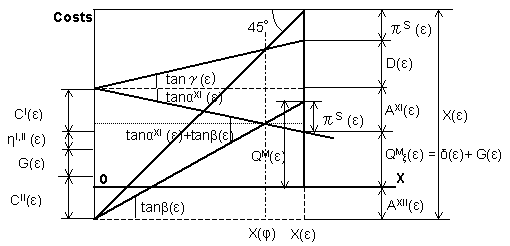
The relationship between the 45° break-even chart and the managed gross profit chart is shown in Fig. 1-5.

Fig.1-5 Relationship between 45° break-even chart and managed gross profit chart

The following equations hold:

tan α^XI (ε) + tan β (ε)=(X (ε) - D^X (ε) ) / X (ε) (1-25)

tan α^XI(ε) + tan β (ε) + tanγ(ε) = 1 (1-26)

π^S(ε) = (X (ε) - X(φ)) ( tan α^XI (ε) + tan β (ε)) (1-27)

Q^M (ε) = π^S(ε) /(1 - Q ^M _ξ (ε) / Q^M (ε)) (1-28)

The author claims the following:

(1) The brake-even sales formula under absorption costing, including standard costing, has been presented by D. Solomons (1968), and now can be found in any accounting textbook. Absorption costing is now used for public disclosure and usually used in firms' accounting. The break-even sales formula by D. Solomons is wrong. A correct formula has been presented by the author( Y. Hayashi) and this is shown in Eq. (1-24).

(2) Two methods transforming an income statement( profit and loss statement) into charts have been presented by the author. The first chart is the 'managed gross profit chart', which is shown in Fig.1- 3. The second chart is the 45° break-even chart, which is shown in Fig. 1-4.

(3) A company adopting standard costing can make a profit plan chart and execute profit or cost control by using the managed gross profit chart in place of direct costing. Until now, the profit planning with chart could only be made by using direct costing.

In conclusion, cost-volume-profit analysis under standard costing (absorption costing or full costing) is possible.

The author's managed gross profit chart theory including the 45-degree break-even chart with inventories will be the essential theory which integrates actual costing, absorption costing, direct costing and costing adopting an intra-company transfer price system. The 45-degree break-even chart will especially be used in accounting textbooks and various theories in economics in the future. On the other hand, the managed gross profit chart will be used in actual business managements because manufacturing direct costs are excluded in the chart expression, and so the profit part is enlarged for the chart to become easily viewable.

In conclusion, cost-volume-profit analysis under standard costing (absorption costing or full costing) is possible.

If this theory is left as it stands now, it will not be effectively utilized in practical management accounting. Therefore, the author will present a paper, in the near future, in which profit management in standard costing is targeted. Better position of standard costing than direct costing in profit management will then be revealed.

References

(1) Yuichiro Hayashi, “Method of Charting Expression for Company’s Profit”, JPO Koukai, No. H9-305677, Unexamined PATPEND, 1997, in Japanese.

(2) Yuichiro Hayashi, "ACCOUNTING SYSTEM FOR ABSORPTION COSTING", US Patent, Patent No.US7,302,409B2, 27,Nov. 2007.

publication　Dec. 2003 　

rewritten　23/July/2008