VNAを用いたQ測定---QDEMOW（QZEROのデモ版）    (2017/09/30)

　QZEROはDarko Kajfez氏が開発したQ解析プログラムで、ベクトルネットワークアナライザ（VNA）で測定した共振器の反射特性データを入力するとそのQ値を計算してくれます。計算の方法はまずスミスチャート上でQサークルの中心点と直径を決定し、そこから負荷Q、結合度、無負荷Qを算出するというものです[1]。QDEMOWというQZEROのデモ版がネット上に見つかりましたので[2]、 さっそくダウンロードして試してみることにしました。デモ版にはデータ数が20個以内という制限がありますが共振点近傍のデータを与えれば無負荷Q（Q0）、負荷Q（QL）、結合度（K）の計算結果が返ってきます。この方法で測定した結果をアンテナアナライザ(AA-30）を用いたコイルのQ測定　(2014/10/31)、追記 (2014/12/14)で述べた簡易な方法と比較してみました。

　

１．測定

　測定対象のLC共振器をFig.1-1に示します。コイルは直径2cm、1mmΦ銅線10回巻き、これに22pFのセラミックコンデンサをハンダ付けしたもので、共振周波数は約30.7MHzとなりました。

　Fig1-1  An LC resonator for test measurement

　測定器はminiVNA-Tinyで、直径5cmのワンターンループをDUT端子に取り付け、インピーダンスを測定しました。共振器とワンターンループの距離を0〜8cmの範囲で変えると結合度：Kは4.2から0.016まで変化しました。

　

２．QDEMOW

　QDEMOWを立ち上げるとFig.2-1のスタートアップ画面が現れます。入力データがインピーダンスの場合、”In”の選択メニューで”f, Re[Zin], Im[Zin]”を選択します。（データファイルには周波数[Hz]、Rs[Ω]、Xs[Ω]をワンセットで1行に記載しますが最大20行までという制限があることは先に述べたとおりです。）また、1-portか2-portかのメニューがありますが反射特性のみ対応しているので1-portしか選択できません。OKボタンを2回クリックするとデータファイルを選択するウィンドウが開くので対象ファイルを指定します。すると瞬時に計算結果が表示されます。Fig.2-2がその一例ですが、Q-サークル上のドットが入力データを示しています。

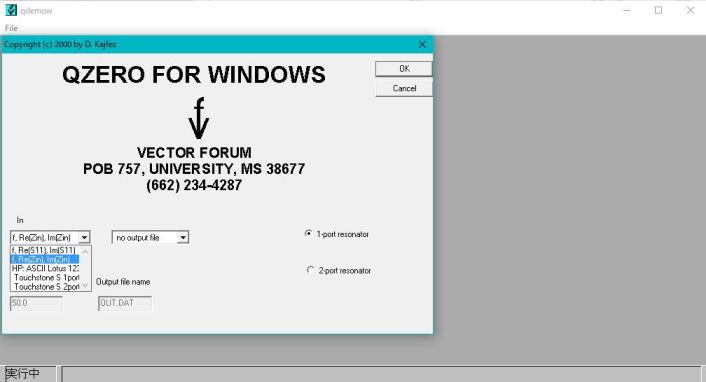
Fig.2-1  Main window of QDEMOW (the demo version of QZERO program)

　

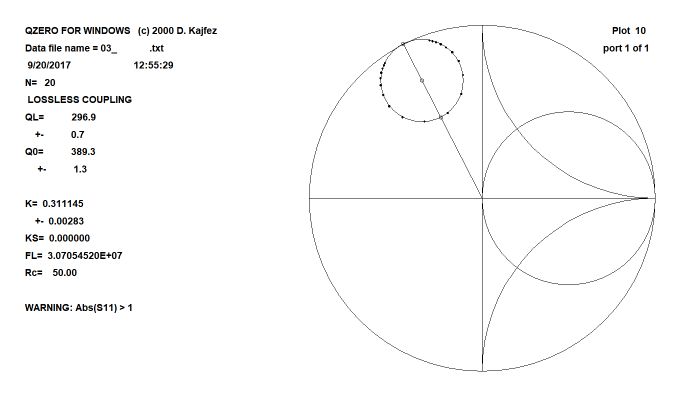
Fig.2-2  An example of QDEMOW calculation result.  Q-circle with the raw data (dots) is displayed on a Smith chart.  The center of the Q-circle is not on the real axis but is rotated clockwise due to the coupling coil inductance.   

QL、Q0、Kの解析結果がウィンドウの左側に表示されます。QLはKの大きさに応じて変化しますがQ0はKに依存しない特性値です。K=1すなわち臨界結合のときはQL=Q0/(1+K)=Q0/2というよく知られた関係になります。Fig.2-3に異なるKに対するQ0の測定結果を示します。

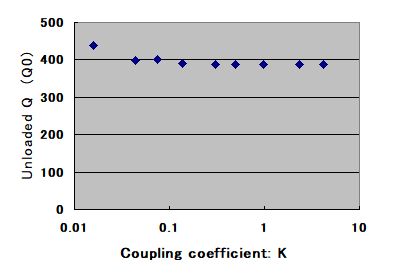
Fig.2-3  Q0 for various K given by QDEMOW

　Kが0.1以上の測定ではQ0=~390でほぼ一定値であることが確認できます。VNAの特性上、測定インピーダンスが50Ωから大きく離れると測定精度が低下するので、実際、K < 0.1では誤差が目立っています。

　

３．Re[Z]半値幅法

　共振器のQ0（無負荷Q）を求める簡便な手法についてこれまで折に触れて紹介してきましたが、ここで簡単にまとめておきます。その方法とは、共振器に結合させたカップリングコイルのインピーダンスを測定し、その実部：Re[Z]にあらわれる共振ピークの半値幅（FWHM）からQ0を算出する、というものです。ここでは便宜上、この手法を”Re[Z]半値幅法”と呼ぶことにします。

　共振ピークが最大値をとる周波数：f0を共振ピークの半値幅で割った値がQ0になることは以下のように説明できます。

　L、Ｃ、Rからなる共振器とカップリングコイル：LCが相互インダクタンス：LXで結合しているとすると、カップリングコイルのインピーダンス：Zは下式で表されます。

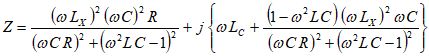
ここで、ω（=2πf）は角周波数です。実部だけを取り出すと

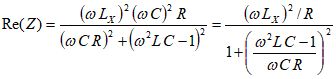
となり、共振曲線はローレンツ型関数であることがわかります。分母の第2項がゼロ、すなわち共振周波数：ω0 （ω02 LC = 1）においてRe[Z]は最大値となります。

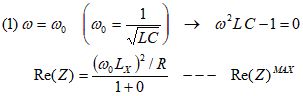
また、分母の第2項が第1項と等しいときRe[Z]は最大値の1/2になり、この周波数幅が半値幅（FWHM）です。

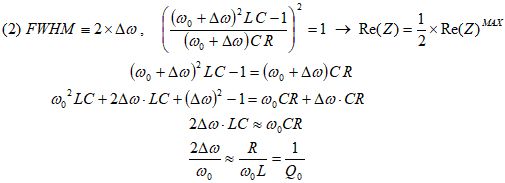
こうして Q0 = ω0 / (2Δω) = f0 / (2Δf) となることを確認できます。（詳しくはこちらを参照）　

　

（注）スカラー測定で|Z| の共振ピークを扱う場合、カップリングコイルのインダクタンスを無視すればω = ω0±Δω ではIm[Z] = ±Re[Z] ですから

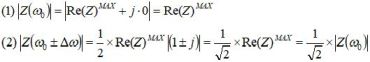
となり、|Z| の最大値の1/√2となる周波数幅 (-3dB幅)がRe[Z]の半値幅(-6dB幅)に対応します。しかし実際のスカラー測定ではカップリングコイルのインダクタンスが加味されるため、|Z| の共振ピークは左右非対称になりローレンツ型関数ではなくなります。これに対しVNAで得られるRe[Z]はカップリングコイルのインダクタンスを含まないので常にローレンツ型となり、半値幅による解析が可能となるわけです。

　

　通常はRe[Z]を共振周波数近傍で細かく測定し共振ピークの中心周波数：f0を半値幅：2Δf で割ればQ0が得られますが、今回は比較のためQDEMOWと同じ粗いデータを用いたのでローレンツ型関数によるカーブフィッティングで半値幅を算出しました。カーブフィッティングにはIgor Proを使いました。（EXCELのソルバーでも出来ないことはないのですが初期値をうまく設定しないと答えが収束しませんでした。）Fig.2-2に対応する解析結果が下図になります。

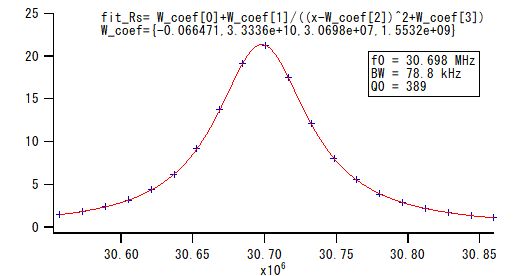
Fig.3-1  Q0 measurement by a simple Re[Z]-FWHM method.  Vertical axis: Re[Z] in ohms, Horizontal axis: frequency in Hz.

横軸は周波数（Hz）、縦軸はRe[Z]（ohm）です。関数の定義により半値幅はFWHM=2×√W_coef[3]で与えられます。QDEMOWと同じQ0値が得られています。さらに異なるKについてもQ0を求め、QDEMOWの結果と比べてみました。

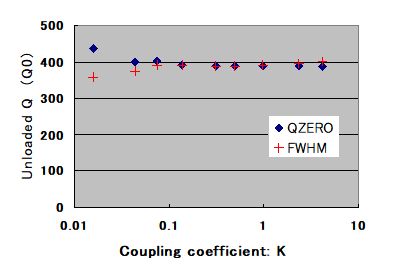
Fig.3-2  Q0 given by Re[Z]-FWHM method and QDEMOW(QZERO)

赤色＋マークが半値幅法の結果を示していますが、QDEMOWとほぼ同じ結果になっています。（K<0.1ではVNAの測定精度が悪化するので誤差が大きくなっていますが、ずれの方向がQDEMOWと逆向きです。）

　

４．まとめ

 QZEROのデモ版を使ってみました。少ないデータ数にもかかわらず安定した解析結果が得られているようです。また、「Re[Z]半値幅法」と勝手に呼んでいる簡便なQ0 解析法でも同等の結果が得られることを確認しました。ただしQZEROでは負荷Q（QL）と結合度（K）を同時に示してくれるので、より確実な解析法であることに間違いありません。

　

REFERENCES

[1] D. Kajfez; "Q factor measurements, analog and digital" , https://engineering.olemiss.edu/~eedarko/experience/rfqmeas2b.pdf

[2] D. Kajfez; Q Factor Measurement with Network Analyzer , http://www.aces-society.org/software.php　

　

 戻る