�߂�
�R �덷��͎�@�ɂ��(�P)
�����ł̓}�g���b�N�X��Ώ̉�������(3-1)�ɕ�����������v�Z���x�̌���Ɛ��l���̈��萫���P��}��B
�R�D�P�@��ʉ��̑������q
����u ���g�U�W��![]() ���萔�̏ꍇ�ɂ͎�(2-1)�͕ϐ������@�ɂ���ĉ���
���萔�̏ꍇ�ɂ͎�(2-1)�͕ϐ������@�ɂ���ĉ���
���Ƃ��ł��A���̈�ʉ��̓t�[���G�����ŕ\������邪�A���̐����̈�͎����ŕ\�����(6)�B
�@�@�@�@�@�@�@![]() �@�@�@�@�@�@�@�@�@�@�@ (3-3)
�@�@�@�@�@�@�@�@�@�@�@ (3-3)
�������AA�F���f�萔�A![]() (
(![]() )�F
)�F![]() �����̔g���C
�����̔g���C![]() �F�������̔g���A
�F�������̔g���A![]() �ł���
�ł���
�i�Ȃ����������Ƌ��E�����������͉������߂�ɂ́A�e�����𑫂����킹�ď���������
�悤�Ɋe������A��![]() ���߂�悢�j�B�����Ŏ��ԕ����ɂ�����=���E��t�ŗ��U��������A
���߂�悢�j�B�����Ŏ��ԕ����ɂ�����=���E��t�ŗ��U��������A
��(3-3)��莞��t=���E��t �ł̐ߓ_![]() �ɂ�����Z�x�����̈�͎����ŕ\�����B
�ɂ�����Z�x�����̈�͎����ŕ\�����B
![]()
![]() �@�@ (3-4)
�@�@ (3-4)
�����ŁA��(3-3)���
![]()
![]() �͑O�̎����ɂ�����
�͑O�̎����ɂ�����
�ߓ_
![]() �ł̔Z�x
�ł̔Z�x![]() �ł��邽�߁A��(3-4)�͎�(3-5)�Ƃ��ĕ\�����D
�ł��邽�߁A��(3-4)�͎�(3-5)�Ƃ��ĕ\�����D
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �@�@�@�@�@
(3-5)
�@�@�@�@�@
(3-5)
������![]() �ł���A�������W��
�ł���A�������W��![]()
![]() �i�N�|�������j��
�i�N�|�������j��
![]() �i�g�U���j������Ǝ�����B
�i�g�U���j������Ǝ�����B
![]() �@�@�@ (3-6)
�@�@�@ (3-6)
�����Ŏ�(3-6)�̎�����![]() �A������
�A������![]() �Ƃ����Ǝ�����B
�Ƃ����Ǝ�����B
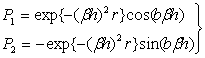 �@�@�@ (3-7)
�@�@�@ (3-7)
�Ȃ���(3-5)����킩��悤�ɁA![]() �͔Z�x�̎��ԕω������肷�邽�ߑ������q�ƌĂ��B
�͔Z�x�̎��ԕω������肷�邽�ߑ������q�ƌĂ��B
�R�D�Q�@�ό`�K�����L���@�̑������q
�ό`�K�����L���@�̐��l���͉�͉����ߎ����ׂ��ł��邱�Ƃ���A
��(3-5)�������`���Ŏ����̂悤�ɕ\�����B
![]() �@�@
(3-8)
�@�@
(3-8)
������![]() �͕ό`�K�����L���@�ł̑������q�ł���D�܂��ߓ_
�͕ό`�K�����L���@�ł̑������q�ł���D�܂��ߓ_![]() �̗אڐߓ_
�̗אڐߓ_![]() (
(![]() )�ł�
)�ł�
���l��![]() ��
��![]() �Ƃ̊W�͊e�ߓ_�ł̈�ʉ��̊Ԃ̊W���Ɠ����`���ɂȂ邽�߁A
�Ƃ̊W�͊e�ߓ_�ł̈�ʉ��̊Ԃ̊W���Ɠ����`���ɂȂ邽�߁A
��ʉ��̎�(3-3)��(3-8)����A�����̂悤�ɕ\�����B
![]()
![]() �@�@�@�@�@�@�@�@ (��(3-3)���)
�@�@�@�@�@�@�@�@ (��(3-3)���)
![]() (��(3-8)���) �@�@�@�@�@�@�@�@�@�@�@ (3-9)
(��(3-8)���) �@�@�@�@�@�@�@�@�@�@�@ (3-9)
��(3-8)��(3-9)��㐔������(3-2)�ɑ�������ӂ�![]() �Ŋ���Z����Ǝ�����������B
�Ŋ���Z����Ǝ�����������B
![]()
![]()
![]() (3-10)
(3-10)
������![]() ���l�����ď㎮������ƈȉ��̑������q��������B
���l�����ď㎮������ƈȉ��̑������q��������B
 �@�@�@�@ (3-11)
�@�@�@�@ (3-11)
���܊ȒP�̂��߂ɕό`�K�����L���@�̑������q�������̌`�ōl����D
�@
�@�@�@�@�@�@
![]() �@ �@�@�@ (3-12)
�@ �@�@�@ (3-12)
�����ŁA![]() �A
�A![]() : ���퍀���琶����A�@
: ���퍀���琶����A�@![]() �A
�A![]() :
: ![]() �̊��ł���C�g�U�����琶����A
�̊��ł���C�g�U�����琶����A![]() :
: ![]() �̊��ł���A
�̊��ł���A
�ڗ������琶������̂ƕ��ނł���B�@���������Ď�(3-11)���![]() �`
�`![]() �͎����̂悤�ɕ\�����B
�͎����̂悤�ɕ\�����B
![]() �@�@
�@�@![]() �@�@
�@�@![]() �@
�@![]() �@
�@![]() �@ (3-13)
�@ (3-13)
�R�D�R�@��W���̓���
���܂��鐔�l��@�̌v�Z���x�����コ���邽�߂Ɋg�U���ƈڗ����̒莮���ɂ�����
��W�����������������D���Ȃ킿��(2-1)�̑���Ɏ�������͑ΏۂƂ��čl����B
![]()
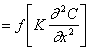 �@�@�@�@�@�@ (3-14)
�@�@�@�@�@�@ (3-14)
���������Ă��̏ꍇ�̕ό`�K�����L���@�̑������q�͈�ʂɎ����̂悤�ɕ\�����B
![]() �@�@�@�@�@
(3-15)
�@�@�@�@�@
(3-15)
���ɕ�W���� f ��g ����ʉ��ɂ����鑝�����q(��(3-6))�ƕ�������l���̑������q
(��(3-15))�Ƃl���邱�Ƃɂ�苁�߂��D���Ȃ킿�����̓������������Ƌ����̓��
�W���ɕ����邱�Ƃɂ��Af �Ƃ� �����߂邱�Ƃ��ł���B
![]()
![]() �@�@�@�@ (3-16)
�@�@�@�@ (3-16)
![]() �A
�A![]() �A
�A![]() �`
�`![]() �͔g��
�͔g��![]() �Ɉˑ����Ă��邪�A�����Ŕg���ɂ��Ȃ���W����
�Ɉˑ����Ă��邪�A�����Ŕg���ɂ��Ȃ���W����
���߂邽�߂ɁA![]() �ł̋Ɍ����l����Ǝ�����������B
�ł̋Ɍ����l����Ǝ�����������B
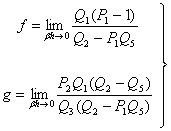 �@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (3-17)
�Ȃ�
![]() �i
�i![]() ,
, ![]() : x�����̔g���j���Ɍ��Ń[���Ƃ���l�����́A�����x�̐��l�������邽�߂�
: x�����̔g���j���Ɍ��Ń[���Ƃ���l�����́A�����x�̐��l�������邽�߂�
�g���ɔ�ׂď\�������ȃ��b�V�������g�p���邱�Ƃɑ�������D�����Ď�(3-17)������߂����@���g�U���ɁA
���@���ڗ����ɂ�����ƁA�ŏI�I�ɕό`�K�����L���@�ɂ��莮���邱�Ƃ��ł���B