(2-21)戻る
2.5 代数方程式のマトリックス表示
式(2-20)の連立方程式は、一般に以下のマトリックス表示で表すことができる。
(2-21)
ここで、
と
は時刻
と
における節点での未知関数
ベクトルであり、各マトリックスを式(2-22)と(2-24)のように求めると、
以下に説明するように式(2-20)と式(2-21)とは等価になる。
まず
は次式で表される。
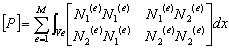(2-22)
ここで各
のマトリックスは要素マトリックスとよばれ、
またVe：要素(
)の領域（
～
の範囲），
,
：要素(ｅ)での形状関数 である。
なお M：総要素数であり、∑は各要素マトリックスを足し加えて
全体マトリックスを作成することを意味している。
式(2-22)の要素マトリックスでは、たとえば一行一列目の成分は
図2-3と式(2-13)より次式で表される。
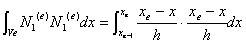
結局、
を考慮して上式を積分すると次式が得られる。
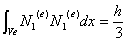(2-23)
同様にマトリックスの他の成分や他のマトリックス
についての定式化の結果は次式で表される。
,
,
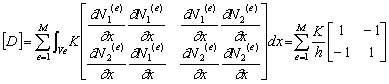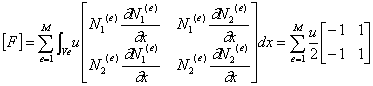(2-24)
また各要素マトリックスの成分を次のように足し加えて全体マトリックスを
作成すると式(2-21)と式(2-20)とは等価になる。たとえば、式(2-24)の
中の
要素（図2-3、
）と
要素(図2-3、
）に対する各マトリックスの
成分は図2-4のように表される。
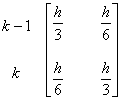
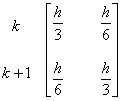
(a) Element (b) Element
Fig.2.4 Element matrices and corresponding nodes
ここで、要素()の一行目の成分は当該要素の一番目の節点()に
関する方程式、すなわちの()行目に寄与する。また二行目の成分は
当該要素の二番目の節点に関する方程式、すなわちの行目に寄与する。
一方、二行一列目の成分（h/6）はの()列目に、二行二列目の成分
（h/3）は()列目に加える。
次に要素（）の要素マトリックスにおける一行一列目の
成分（h/3）をの行列目に、一行二列目の成分（h/6）を行()列目に
加える。二行目の成分はの()行目に寄与し、それ以外の要素からの
第行目への寄与はゼロである。その結果、
の第行目は
となる。
またマトリックス
と
についても同様に作成し、両辺に
をかけて
無次元係数を導入すると
行目の代数方程式として式(2-20)を得る。以上の
節点に関する議論をすべての内部節点（ 節点に対して節点 ()と()が
存在 ）に適用し境界条件を導入すると未知関数値の個数と同数の連立方程式が
得られるため、これを解いて各節点値を求めることができる。
上述のガレルキン法は有限要素法の最も基本的な一種であるが、流体解析では
一般に数値振動が発生するため、前述の各種の安定化解法が適用されている(1),(2)。
また移流項に関するマトリックス
は非対称となり、連立方程式の解法では
対称マトリックスのみの場合に比べてより多くの計算時間と計算容量を必要とする。
これらの問題を解決するため著者らは次章で述べる変形ガレルキン法を提案した。