戻る


2.4 各節点に関する代数方程式

式(2-12)〜(2-14)を式(2-5)に代入して積分すると節点に

　　関する代数方程式が得られる。まず式(2-5)の第１項について考えると、

　　式(2-14)より　と　において　であるため次式を得る。

　


次に上式に式(2-14)を代入して次式を得る。

　したがって式(2-13)を代入して次式を得る。

　
結局、上式を積分して次式を得る。

 


これをマトリックス表示すると次式が得られる。
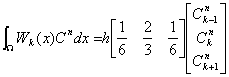　　　　 　　　　　　         　    (2-15)

同様に次式が得られる。

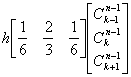　　　　　　　　　　　     　       (2-16)

　

また式(2-5)の移流項については以下の式を得る。

　ただしここでは簡単のために時間方向の添字は省略している。

まず式(2-14)のの定義範囲から次式を得る。

　ここで流速は各要素内で一定としているため、積分の外に出ている。

　　次に式(2-14)の定義から次式が得られる。ただし、である。

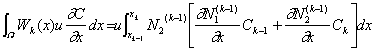
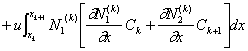
したがって式(2-13)から次式を得る。

　　
　 結局、この積分を実行して次式を得る。

すなわちマトリックス表示すると次式が得られる。
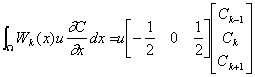　　　　　　　　　　　    　　　　   (2-17)

　　　　また式(2-5)の拡散項については次式の部分積分を考慮する。

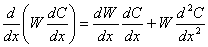　　　 　　　　　　　        　　　    (2-18)


　すなわち、式(2-14)より次式を得る。



　　　
よって、式(2-18)より次式を得る。

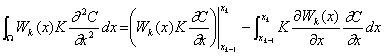
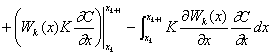
ここで式(2-14)より、、 及び　　なので

　　　上式右辺の第１項と第３項は相殺され、結局、次式が得られる。  

また式(2-14)と(2-12)から次式を得る。

　　


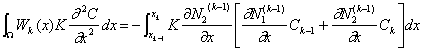
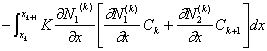
すなわち式(2-13)を代入して積分すると次式が得られる。
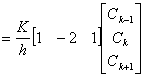　　　　　   　     (2-19)

　式(2-15)〜(2-17)と(2-19)を式(2-5)に代入し、両辺にをかけて

無次元係数の(ク−ラン数)　と（拡散数）を導入して整理すると、

次のような節点に関する代数方程式が得られる。

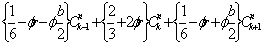
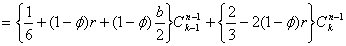
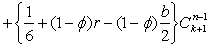　　　　　　　　　　　　　　　 　　　     　　　 (2-20)

他の内部節点についても同様な代数方程式が得られ、これらの

代数方程式を連立させ、境界条件を考慮して解くと各節点値が求められる。

以 上