戻る

2.3 形状関数と重み関数

いま図2-1のように一次元座標 x において節点１と節点２を考え、この２節点に

囲まれた領域 （“一次元要素”とよぶ）における任意の位置（ 印）での

未知関数を次式により定義する。

　　　　　　　  　　    (2-6)

なお以下では簡単のために式(2-6)の代りに次式のように表記する。

          　　       (2-7)

ｈ　　　　　

　　　　　　　１              ２        　 　　  

  Fig. 2-1 One-dimensional coordinator

　　　　　　　　　　　　　ここで、はこの要素での補間関数であり、下記の理由から形状関数とも
　　　　　　　　　
　　　　　　　　　　　　よばれる。いま最も簡単な形状関数として次式のような の１次関数を考える。

　　　　　　　　　　　　　　　　　　　　　　　　　　       　　　　　       (2-8)

　　　　　　　　　　 ここで と は決定すべき４個の未知係数である。一方、図2-1での任意点（ 点）を

　　　　　　　　　　　　　　　　　　　　節点１に移動させると、式(2-6)から次の関係式を得る。

、    　　　　         (2-9)

　　　　　　　　　　　　　　同様に 点を節点２に移動させて考えると式(2-6)から次式を得る。

   　　　　　　　　　 　         、      　 　    (2-10)


　　　　　　　　　　　　すなわち式(2-9)と(2-10)の４個の関係式が得られるため、これを解いて

　　　　　　　　　　　　　　　　　　　　結局４個の未知係数が以下のように求まる。

 　　　　　　　　　　 、、、　（ただしである。）

　 　　 　 　　　　　　　　　　　　　　　 すなわち式(2-8)より次式を得る。

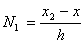
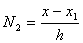　　　　　　　　　　　　　　　　　 　　　　 　　　　    　      (2-11)

　　　　　　　　 図2-2に各関数のによる変化を示すが、これより、は各々、右下がりと
　
　　　　　　　　　　　 右上がりの“特別な形状”に対応することから“形状関数”ともよばれる。

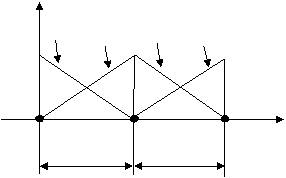
　　　　　　　図2-3は、より一般的に節点、、の３点を考えた場合であるが、ここで節点と、

　　　　　　　　　　　およびとで囲まれた要素領域を各々ととで表す。ただし各節点間の

　　　　　　　　　　　　　　　　　　　　　　長さは簡単のために一定としている。
　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　            　　　      
　　　　　　　　　　　　　　　　　　　　　　　  １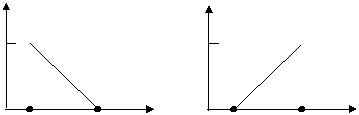
     　　　　　　　　　　　　　　　　　　　　　　                 　　           

　　　     Fig. 2-2 Shape functions

　 　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　 　 　(k-1)       (k)　

Fig. 2-3 Shape functions in elements

　　　　　　　　　　　　　　 　　　 したがって各要素でのと各形状関数は次式のように表される。

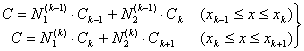　　　　　　　　　　　　　　　　　　　　　　　　　    　　　　　    (2-12)

ただし以下の関係式が成り立つ。

      、　 、   、　         (2-13)

　ここでガレルキン法の場合には重み関数として形状関数と同じ関数をとるため、

結局、次式を得る。
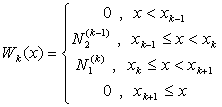　　　　　　　　　　　　　     　　　　   　　   (2-14)

　すなわち重み関数は各要素ごとでの線形関数で、節点では１、他の節点では

ゼロの値をとる。　またその全領域にわたる積分値は１である。