微分方程式を代数方程式に変換し、各節点での未知関数値を求める。
すなわち節点
元の微分方程式の各項に重み関数をかけて全計算領域
積分する。したがって式(2-1)の方程式では次式を得る。
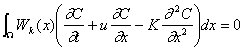 (2-2)
(2-2)まず式(2-2)の時間微分項を離散化するために以下の関係式を考える。
ここで、
次に式(2-3)において式(2-4)の差分関係式を代入すると、
時間微分項を消去した式(2-5)を得る。
戻る
2.2 重み付き残差法とガレルキン法
有限要素法では重み付き残差法の考え方により解くべき
微分方程式を代数方程式に変換し、各節点での未知関数値を求める。
すなわち節点![]() での未知関数値に関する代数方程式を得るために
での未知関数値に関する代数方程式を得るために
元の微分方程式の各項に重み関数をかけて全計算領域![]() について
について
積分する。したがって式(2-1)の方程式では次式を得る。
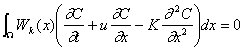 (2-2)
(2-2)
まず式(2-2)の時間微分項を離散化するために以下の関係式を考える。
![]()
![]() 時刻での式(2-2)の左辺}+
時刻での式(2-2)の左辺}+![]()
![]() 時刻での式(2-2)の左辺}
時刻での式(2-2)の左辺}![]() (2-3)
(2-3)
ここで、![]() はタイム・スキーム・パラメータとよばれる。
はタイム・スキーム・パラメータとよばれる。
次に式(2-3)において式(2-4)の差分関係式を代入すると、
時間微分項を消去した式(2-5)を得る。
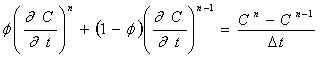 (2-4)
(2-4)
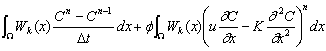
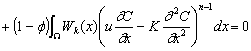 (2-5)
(2-5)
ここで、![]() は時間方向の指標、
は時間方向の指標、![]() はタイム・ステップであり、
はタイム・ステップであり、![]() は
は![]() 時刻目での
時刻目での![]() の値を示す。
の値を示す。
また、![]() の値が0の場合は陽的スキ−ム、0.5の場合はクランク・ニコルソン・スキ−ム、
の値が0の場合は陽的スキ−ム、0.5の場合はクランク・ニコルソン・スキ−ム、
1の場合は完全陰的スキ−ムに対応する。