戻る

^{１．３　不等長間隔メッシュにおける誤差解析手法の導入}

　式(1-2)において流速 u , v 及び拡散係数 が定数である場合、

この式は変数分離法によって解くことができ、その一般解はフーリエ級数で表現される。

離散化の結果一般解における増幅因子は次式のようになる。

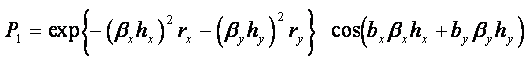
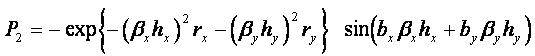
　ここで、　　Ａ：複素定数　　βｘ,βｙ：ｘ,ｙ方向の波数（＝2π／λ）　

λ：フ−リエ成分解の波長（−∞〜＋∞）

　　　ｔ＝nΔｔ, 　　　ｘ＝ｎｘｈｘ，ｙ＝ｎｙｈｙ　　　クーラン数：ｂｘ＝ｕΔｔ／ｈｘ，ｂｙ＝ｖΔｔ／ｈｙ

　　　フーリエ数：ｒｘ＝ＫΔｔ／ｈｘ^２，ｒｙ＝ＫΔｔ／ｈｙ^２

　　　（ ただし、ｎｘ,ｎｙ：ｘ,ｙ方向の指標，ｈｘ,ｈｙ：ｘ,ｙ方向のメッシュ幅，Δｔ：タイム・ステップ ）　とする。

いっぽう、FWA法の増幅因子は次式のように表される^（１）。

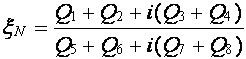
ここで、　Ｑ１,Ｑ３,Ｑ５,Ｑ７:ｒｘ,ｒｙとβｘｈｘ,βｙｈｙの関数

　Ｑ２,Ｑ４,Ｑ６,Ｑ８:ｂｘ,ｂｙとβｘｈｘ,βｙｈｙの関数　である。

　　式（１-5）のような不等長メッシュについての定式化におけるＱ１〜Ｑ８を次式により

　表すことができる。

また、，　である。

   （hi=Hihx，hj=Hjhy，ここで、hxおよび hyは“代表長さ”である。）

ただし、ａ(i)〜ｅ(i),ａ(j)〜ｅ(j),ａ(i)*〜ｅ(i)*,ａ(j)*〜ｅ(j)*は以下の通りとする。

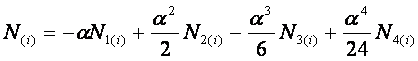
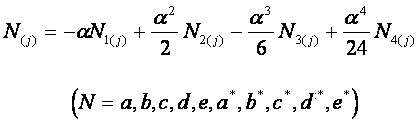
　いま数値解の精度向上のために拡散項と移流項に補正係数ｆおよびｇを導入し、

次式のような補正されたξＮ（Ｃ）を考える。

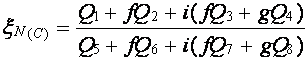　　　　　　　 (1-10)

　よって補正係数ｆとｇは式(1-7)と式(1-9)とを等置することにより求めることができるが、この際

βｘｈｘ,βｙｈｙに依存しない係数を求めるためにβｘｈｘ →０，βｙｈｙ →０の極限を考えると次式を得る。

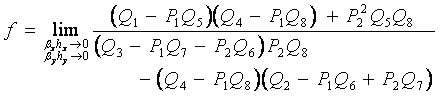　　　　　(1-11)

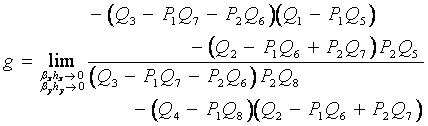　　　　　  (1-12)

　したがって式(3-10)，(3-11)で求めたｆとｇを拡散項と移流項に適用することにより、

数値解法を補正することができる。　以上の結果、不等長間隔メッシュを用いたFWAの

補正係数を次式のように得ることができる。

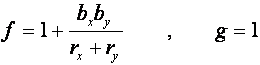  　　　　　 　　　　　　　　　　　 　(1-13)

　式(3-11)の補正係数をFWAに導入した方式をFWA(C)と定義する。

２　数値計算例

２．１　数値計算の一覧

　　計算パラメータおよび数値計算結果（Ra=10⁵〜Ra=10⁷）　　     

　　　　　　　　　　　　　　　　　　　　　　
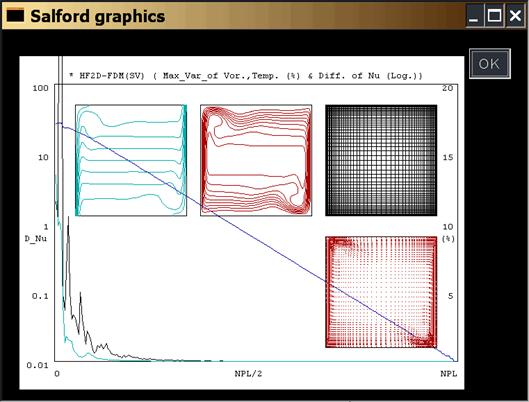
　　　　　　　　　　　　　　　　　　　　　　　　２．２　数値計算例


　　　　　　　　　　

参考文献

（１）松田 安弘・三木 英敬，四次差分法による非定常二次元粘性流の解析
　　　（誤差解析手法によるアプローチ)，日本機械学会論文集，
　　　　　　　60-577，B(1994)，3032．

（２）Woods, L. C.,“A Note on the Numerical Solution of Forth Order
　　　Differencial Equation”，Aeronaut. Q., 5-3(1954), 176.

（３）岡永・棚橋，日本機械学会論文集，56-530, B(1990), 2922.

（４）松田 安弘、他３名，四次差分法による二次元自然対流問題の解析（不等長間隔
　　メッシュの場合），日本機械学会論文集，64-617，B(1998)，10.

（６）邵 長城，松田 安弘・他１名，四次差分法による二次元自然対流問題の解析
　　　　（第2報 高レーリー数の場合），日本機械学会論文集，66-642，B(2000)，332.

以 上